Introduction to Cross-Validation#
Cross-validation is a method that allows precise evaluation of a deep learning model on the entire set of available training data. This course is inspired by the blog post, and the figures used also come from this blog post.
Problems with Deep Learning Models#
As previously mentioned, one of the problems with deep learning models is overfitting. To learn more about overfitting, you can refer to the bonus course on regularization. It is not enough to have a model that performs well on training data; it must also perform well on test data.
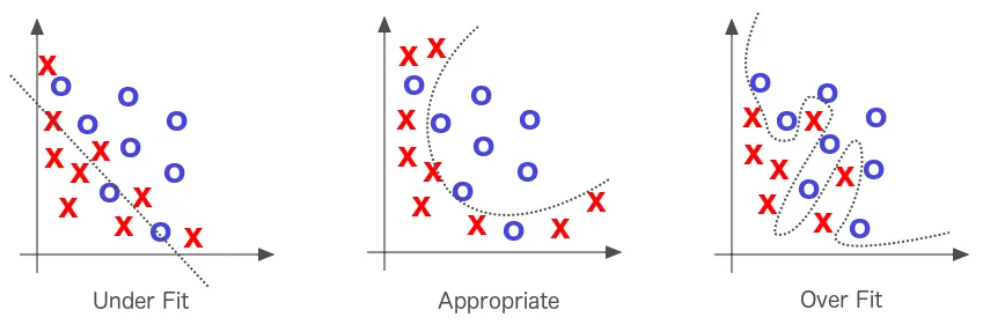
Cross-validation is a technique that makes it easier to detect overfitting and precisely adjust hyperparameters to combat this issue.
How Does Cross-Validation Work?#
The cross-validation technique can be broken down into 3 phases:
We partition our dataset into a chosen number of subsets.
We set aside one of the subsets and train the model on the remaining subsets.
We finally test the model on the subset that was set aside for training.
We repeat the last two steps until all subsets have been evaluated. If we split our dataset into 10 subsets, we will need to train the model 10 times. Once all training is complete, we can evaluate the model by averaging its performance across the different training sessions.
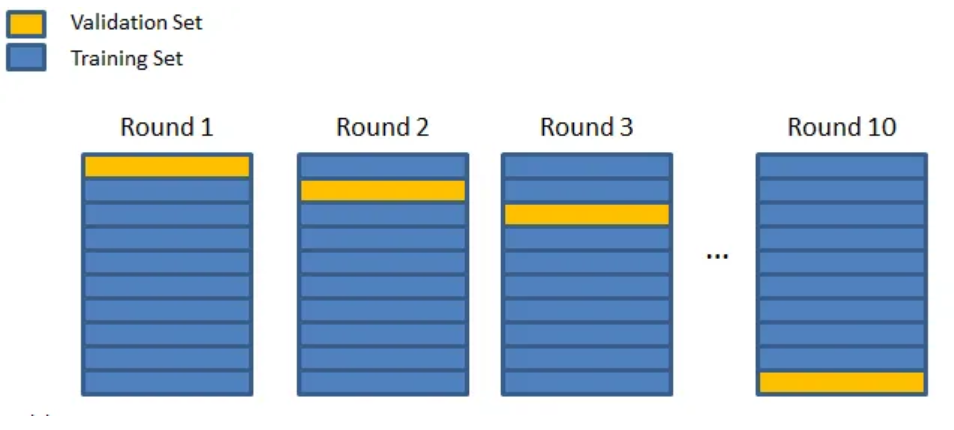
There are 3 types of cross-validation that are quite similar to each other: k-fold cross-validation, stratified k-fold cross-validation, and leave-one-out cross-validation (LOOCV).
K-Fold Cross-Validation#
K-fold cross-validation is the most classic version. We divide our dataset into k subsets. We train k models each time with a different validation subset and average the scores to generally evaluate the model.

How to choose the parameter k: Generally, we choose k so that the subsets are large enough to statistically represent the original dataset. The choice of k also depends on the available time and resources, as the larger k is, the more training sessions we need to perform.
Generally, k=10 is a good value.
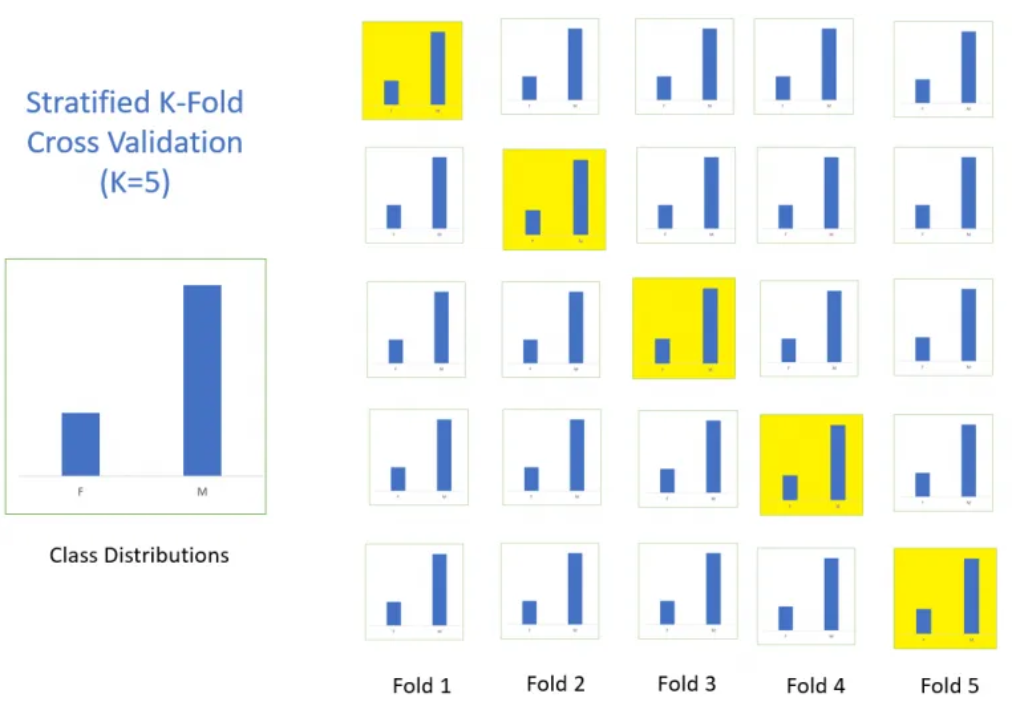
Stratified K-Fold Cross-Validation#
This method is almost identical to basic k-fold cross-validation, but with an added constraint. We specify that each subset must have the same class distribution. This allows us to evaluate each subset on an equal footing in terms of performance relative to each class.
Leave-One-Out Cross-Validation#
Once again, this method is very similar to classic k-fold cross-validation, as it is simply this method with k=n (where n is the size of the dataset). Each time, we train the model on all data except one. This means training the model n times, which can quickly become time-consuming and resource-intensive. The advantage of this method is that we can train the model on almost all of the dataset’s data. In practice, this method is not used much, except in cases where we perform fine-tuning on a small amount of data (and at that point, it is very useful).
Advantages and Benefits of Cross-Validation#
Cross-validation has several advantages:
It makes it easier to detect overfitting, and we can adjust hyperparameters accordingly.
In a scientific context, evaluating models with cross-validation allows for more reliable evaluation and reduces the element of chance (which we might have when randomly separating our training and validation data).
If you can afford it (enough time and computing resources), I invite you to use cross-validation systematically.