Knowledge Distillation#
The concept of knowledge distillation was introduced in the 2015 paper Distilling the Knowledge in a Neural Network. The idea is to use a model called the teacher (a pre-trained deep model) to transfer its knowledge to a smaller model called the student.
How It Works#
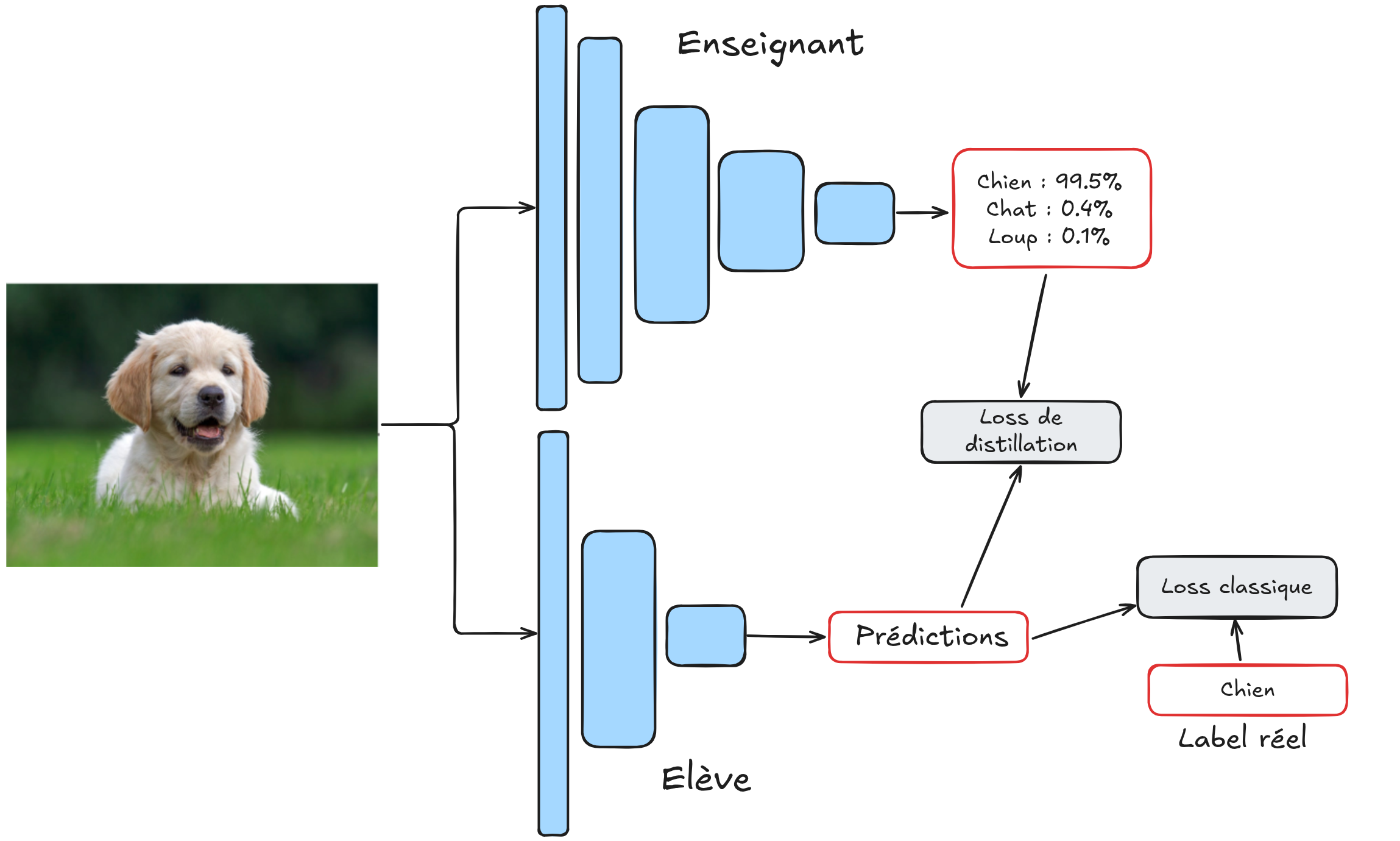
In practice, the student model is trained on two objectives:
Minimizing the distance between its prediction and the teacher’s prediction for the same item.
Minimizing the distance between its prediction and the input label.
These two losses are combined with a weighting factor \(\alpha\) that can be chosen. Thus, the student model uses both the image label and the teacher’s prediction (a probability distribution).
Note: In practice, for the first part of the loss, the logits are compared before applying the softmax function rather than the probabilities. For clarity, we will use the term “predictions” instead of “logits”.
Why It Works#
One might wonder why this method works better than directly training the student with a classic prediction/label loss. Several reasons explain this:
Transfer of Implicit Knowledge: Using the teacher’s predictions allows the student to learn implicit knowledge about the data. The teacher’s prediction is a probability distribution that indicates the similarity between several classes, for example.
Preservation of Complex Relationships: The teacher is very complex and can capture complex structures in the data, which may not be the case for a smaller model trained from scratch. Distillation allows the student to learn these complex relationships more easily, while improving speed and reducing memory usage (as it is a smaller model).
Training Stabilization: In practice, training is more stable for the student with this distillation method.
Mitigation of Annotation Issues: The teacher has learned to generalize and can predict correctly, even if it was trained on images with incorrect labels. In the context of distillation, the significant difference between the teacher’s output and the label provides additional information to the student about the data quality.
Practical Applications#
In practice, it is possible to transfer the knowledge from a high-performing model to a smaller one without significant loss of prediction quality. This is very useful for reducing model size, for example, for embedded applications or CPU processing. It is also possible to distill multiple teachers into a single student. In some cases, the student can even outperform each teacher individually.
This is a useful technique to know for many situations.
Other Applications#
Since its invention, knowledge distillation has been adapted to solve various problems. We present two examples here: improving classification with NoisyStudent and unsupervised anomaly detection with STPM.
Noisy Student: Improving Classification#
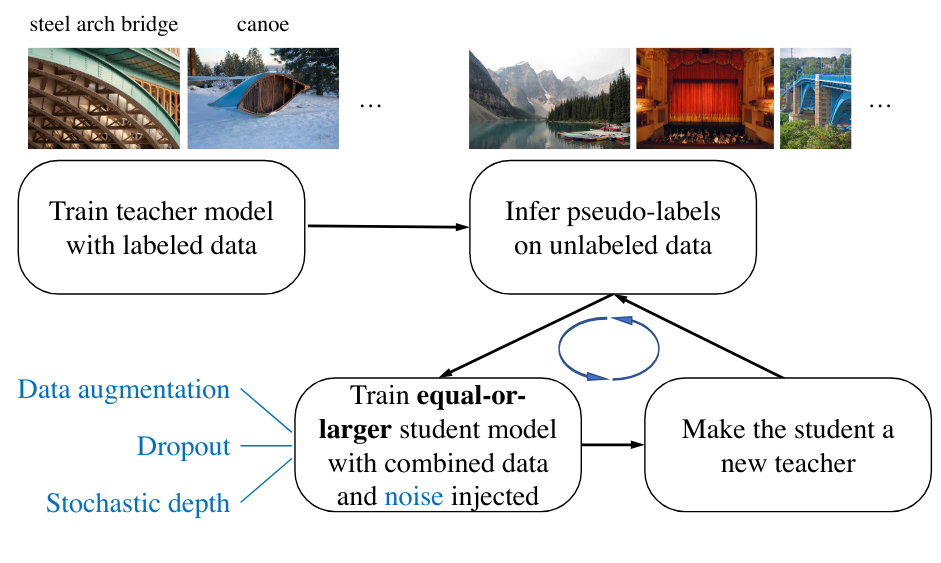
For a long time, the race for performance on the ImageNet dataset was at the heart of deep learning research. The goal was to constantly improve performance on this dataset. In 2020, the paper Self-training with Noisy Student improves ImageNet classification proposes using distillation to train a student model that is more performant than the teacher at each iteration.
A student model is trained from pseudo-labels generated by a teacher model (labels created by the teacher on unannotated images). During training, noise is added to increase its robustness. Once the student is trained, it is used to obtain new pseudo-labels and train another student. The process is repeated several times, resulting in a model that is far more performant than the original teacher.
STPM: Unsupervised Anomaly Detection#
An interesting application of knowledge distillation is unsupervised anomaly detection. The paper Student-Teacher Feature Pyramid Matching for Anomaly Detection adapts this technique for this use case.
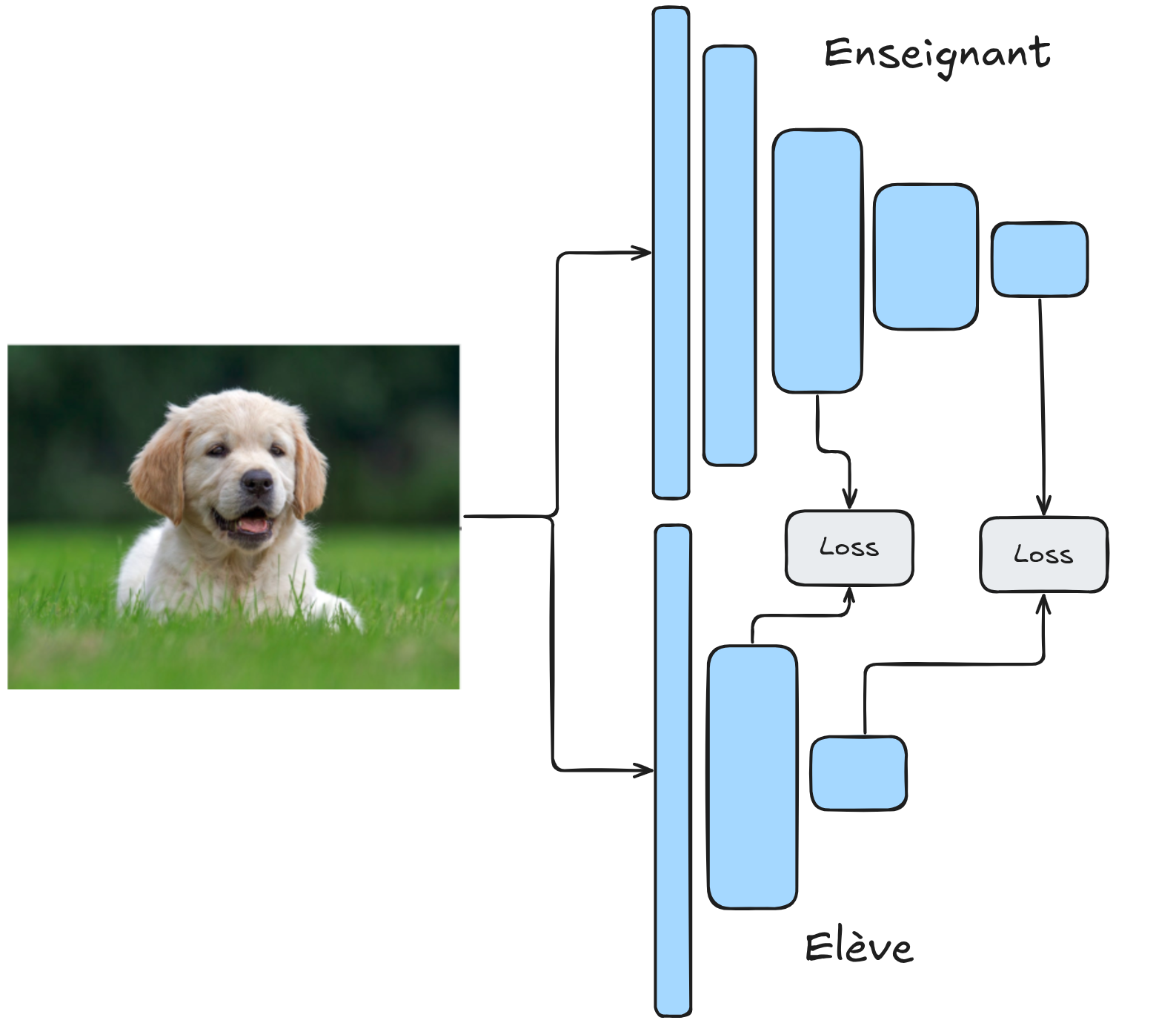
In this case, the teacher and student models have the same architecture. Instead of focusing on predictions, we are interested in the feature maps of the intermediate layers of the network. During training, we have data without anomalies. The teacher model is pre-trained on ImageNet (for example) and is frozen during training. The student model is randomly initialized and is the one we train. Specifically, we train it to reproduce the feature maps of the teacher on defect-free data. At the end of training, the student and teacher will have identical feature maps on a defect-free item.
During the testing phase, the model is evaluated on defect-free data and data with defects. On defect-free data, the student perfectly mimics the teacher, while on defective data, the feature maps of the student and teacher differ. This allows calculating a similarity score, which serves as an anomaly score.
In practice, this method is one of the most performant for unsupervised anomaly detection. This is the method we will implement in the following notebook.