批量归一化

批量归一化#

**批量归一化（Batch Normalization）**于 2015 年在论文 Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift 中被提出，对深度学习领域产生了重大影响。如今，归一化技术（如 BatchNorm、LayerNorm 或 GroupNorm 等）几乎已成为标准操作。

核心思想：批量归一化的目标是确保网络每一层的预激活值（pre-activations）服从高斯分布。虽然良好的初始化能达到这一效果，但在多层网络中难以保证。批量归一化通过对 batch 维度上的预激活值进行归一化，在传入激活函数前确保其分布接近高斯分布。

优点：

该归一化是可导的，不影响模型的优化过程。
通过减少内部协变量偏移（Internal Covariate Shift），加速训练并提升稳定性。

实现#

代码回顾#

我们将基于上一节的代码实现 批量归一化。

import torch
import torch.nn.functional as F
%matplotlib inline

words = open('../05_NLP/prenoms.txt', 'r').read().splitlines()
chars = sorted(list(set(''.join(words))))
stoi = {s:i+1 for i,s in enumerate(chars)}
stoi['.'] = 0
itos = {i:s for s,i in stoi.items()}

block_size = 3 # Contexte

def build_dataset(words):  
  X, Y = [], []
  
  for w in words:
    context = [0] * block_size
    for ch in w + '.':
      ix = stoi[ch]
      X.append(context)
      Y.append(ix)
      context = context[1:] + [ix] 

  X = torch.tensor(X)
  Y = torch.tensor(Y)
  print(X.shape, Y.shape)
  return X, Y

import random
random.seed(42)
random.shuffle(words)
n1 = int(0.8*len(words))
n2 = int(0.9*len(words))

Xtr,  Ytr  = build_dataset(words[:n1])     # 80%
Xdev, Ydev = build_dataset(words[n1:n2])   # 10%
Xte,  Yte  = build_dataset(words[n2:])     # 10%

torch.Size([180834, 3]) torch.Size([180834])
torch.Size([22852, 3]) torch.Size([22852])
torch.Size([22639, 3]) torch.Size([22639])

embed_dim=10 # Dimension de l'embedding de C
hidden_dim=200 # Dimension de la couche cachée

C = torch.randn((46, embed_dim))
W1 = torch.randn((block_size*embed_dim, hidden_dim))*0.01 # On initialise les poids à une petite valeur
b1 = torch.randn(hidden_dim) *0 # On initialise les biais à 0
W2 = torch.randn((hidden_dim, 46))*0.01
b2 = torch.randn(46)*0 
parameters = [C, W1, b1, W2, b2]
for p in parameters:
  p.requires_grad = True

以下是前向传播的代码：

batch_size = 32

ix = torch.randint(0, Xtr.shape[0], (batch_size,))
  
# Forward
Xb, Yb = Xtr[ix], Ytr[ix] 
emb = C[Xb] 
embcat = emb.view(emb.shape[0], -1)
hpreact = embcat @ W1 + b1 

h = torch.tanh(hpreact) 
logits = h @ W2 + b2 
loss = F.cross_entropy(logits, Yb)

批量归一化的实现#

根据论文，批量归一化的步骤如下：

归一化流程

第一步：归一化

计算预激活值 hpreact 的均值（\(\mu\)）和标准差（\(\sigma\)）。
使用以下公式对 hpreact 进行归一化： \( \hat{h} = \frac{h_{preact} - \mu}{\sigma + \epsilon} \) （\(\epsilon\) 为小常数，避免分母为零）

epsilon=1e-6
hpreact_mean = hpreact.mean(dim=0, keepdim=True)
hpreact_std= hpreact.std(dim=0, keepdim=True)
hpreact_norm = (hpreact - hpreact_mean) / (hpreact_std+epsilon)

第二步：集成到前向传播 将上述归一化步骤嵌入前向传播中。

缩放与平移（Scale and Shift） 归一化后的数据服从标准高斯分布（均值 0，方差 1），但这会限制模型的表达能力。为此，引入两个可学习参数：

\(\gamma\)（缩放）：调整数据的方差。
\(\beta\)（平移）：调整数据的均值。

缩放与平移

公式： \( y = \gamma \hat{h} + \beta \)

注意：\(\gamma\) 和 \(\beta\) 需作为模型参数进行优化。

C = torch.randn((46, embed_dim))
W1 = torch.randn((block_size*embed_dim, hidden_dim))*0.01 # On initialise les poids à une petite valeur
b1 = torch.randn(hidden_dim) *0 # On initialise les biais à 0
W2 = torch.randn((hidden_dim, 46))*0.01
b2 = torch.randn(46)*0 
# Paramètres de batch normalization
bngain = torch.ones((1, hidden_dim))
bnbias = torch.zeros((1, hidden_dim))

parameters = [C, W1, b1, W2, b2, bngain, bnbias]
for p in parameters:
  p.requires_grad = True

前向传播的最终表达式为：

batch_size = 32

ix = torch.randint(0, Xtr.shape[0], (batch_size,))
  
# Forward
Xb, Yb = Xtr[ix], Ytr[ix] 
emb = C[Xb] 
embcat = emb.view(emb.shape[0], -1)
hpreact = embcat @ W1 + b1 

# Batch normalization
bnmean = hpreact.mean(0, keepdim=True)
bnstd = hpreact.std(0, keepdim=True)
hpreact = bngain * (hpreact - bnmean) / bnstd + bnbias

h = torch.tanh(hpreact) 
logits = h @ W2 + b2 
loss = F.cross_entropy(logits, Yb)

批量归一化的潜在问题#

批量归一化在实践中可能面临以下挑战：

1. 批次内依赖性

归一化基于 batch 维度进行，意味着每个样本的归一化结果会受同批次其他样本影响。
影响：
- 理论上可能引入噪声，但实践中这种随机性反而起到 正则化 作用，减少过拟合风险。
- 若希望避免批次依赖，可使用 LayerNorm 或 GroupNorm 等替代方案。但 BatchNorm 仍因经验效果佳而广泛应用。

2. 训练与推理不一致

训练阶段：样本的归一化依赖于批次内其他样本的统计量（均值/方差）。
推理阶段：单个样本无法计算批次统计量，导致行为不一致。

解决方案：

指数移动平均（EMA）：在训练过程中动态更新全局均值/方差的估计值，避免额外遍历数据集。实现示例（Python）：
```
# 伪代码：EMA 更新
running_mean = momentum * running_mean + (1 - momentum) * batch_mean
running_var  = momentum * running_var  + (1 - momentum) * batch_var
```
- momentum 典型值为 0.1（PyTorch 默认值），可根据批次大小与数据集规模调整。

C = torch.randn((46, embed_dim))
W1 = torch.randn((block_size*embed_dim, hidden_dim))*0.01 # On initialise les poids à une petite valeur
b1 = torch.randn(hidden_dim) *0 # On initialise les biais à 0
W2 = torch.randn((hidden_dim, 46))*0.01
b2 = torch.randn(46)*0 
# Paramètres de batch normalization
bngain = torch.ones((1, hidden_dim))
bnbias = torch.zeros((1, hidden_dim))
bnmean_running = torch.zeros((1, hidden_dim))
bnstd_running = torch.ones((1, hidden_dim))

parameters = [C, W1, b1, W2, b2, bngain, bnbias]
for p in parameters:
  p.requires_grad = True

batch_size = 32

ix = torch.randint(0, Xtr.shape[0], (batch_size,))
  
# Forward
Xb, Yb = Xtr[ix], Ytr[ix] 
emb = C[Xb] 
embcat = emb.view(emb.shape[0], -1)
hpreact = embcat @ W1 + b1 

# Batch normalization
bnmeani = hpreact.mean(0, keepdim=True)
bnstdi = hpreact.std(0, keepdim=True)
hpreact = bngain * (hpreact - bnmeani) / bnstdi + bnbias
with torch.no_grad(): # On ne veut pas calculer de gradient pour ces opérations
    bnmean_running = 0.999 * bnmean_running + 0.001 * bnmeani
    bnstd_running = 0.999 * bnstd_running + 0.001 * bnstdi

h = torch.tanh(hpreact) 
logits = h @ W2 + b2 
loss = F.cross_entropy(logits, Yb)

注意：

在我们的实现中，EMA 的 momentum 设为 0.001。
PyTorch 的 BatchNorm 层默认 momentum=0.1。
选择建议：
- 大批次 + 小数据集：可使用较大值（如 0.1）。
- 小批次 + 大数据集：建议使用较小值（如 0.001），以更精确地估计全局统计量。

现在我们训练模型，验证批量归一化层的功能。注意：在小型模型中，性能差异可能不明显。

lossi = []
max_steps = 200000

for i in range(max_steps):
  ix = torch.randint(0, Xtr.shape[0], (batch_size,))
  Xb, Yb = Xtr[ix], Ytr[ix] 
  emb = C[Xb] 
  embcat = emb.view(emb.shape[0], -1)
  hpreact = embcat @ W1 + b1 
  
  # Batch normalization
  bnmeani = hpreact.mean(0, keepdim=True)
  bnstdi = hpreact.std(0, keepdim=True)
  hpreact = bngain * (hpreact - bnmeani) / bnstdi + bnbias
  with torch.no_grad(): # On ne veut pas calculer de gradient pour ces opérations
      bnmean_running = 0.999 * bnmean_running + 0.001 * bnmeani
      bnstd_running = 0.999 * bnstd_running + 0.001 * bnstdi
    
  h = torch.tanh(hpreact) 
  logits = h @ W2 + b2 
  loss = F.cross_entropy(logits, Yb)
  
  for p in parameters:
    p.grad = None
  loss.backward()
  lr = 0.1 if i < 100000 else 0.01 
  for p in parameters:
    p.data += -lr * p.grad
  if i % 10000 == 0:
    print(f'{i:7d}/{max_steps:7d}: {loss.item():.4f}')
  lossi.append(loss.log10().item())

      0/ 200000: 3.8241
  10000/ 200000: 1.9756
  20000/ 200000: 2.7151
  30000/ 200000: 2.3287
  40000/ 200000: 2.1411
  50000/ 200000: 2.3207
  60000/ 200000: 2.3250
  70000/ 200000: 2.0320
  80000/ 200000: 2.0615
  90000/ 200000: 2.2468
 100000/ 200000: 2.2081
 110000/ 200000: 2.1418
 120000/ 200000: 1.9665
 130000/ 200000: 1.8572
 140000/ 200000: 2.0577
 150000/ 200000: 2.1804
 160000/ 200000: 1.8604
 170000/ 200000: 1.9810
 180000/ 200000: 1.8228
 190000/ 200000: 1.9977

补充说明#

1. 偏置（Bias）的作用

批量归一化通过 中心化 预激活值，使得偏置项（bias）失去作用（因其仅平移分布）。
实践建议：
- 可移除偏置项，减少参数数量。
- 保留偏置项也不影响模型，但会增加冗余参数。

2. 批量归一化的位置

理论位置：应置于激活函数之前，以归一化预激活值。
实践变体：部分研究/代码将其置于激活函数之后，需根据具体框架灵活调整。

其他归一化方法#

除批量归一化外，深度学习中常用的归一化方法还包括：

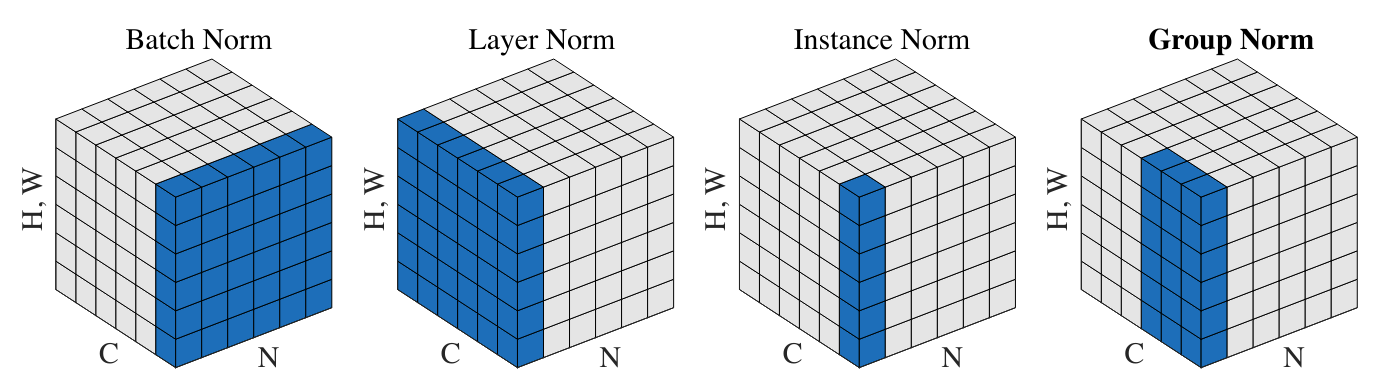归一化方法对比 图片来源：文章

1. 层归一化（Layer Normalization）

应用场景：广泛用于语言模型（如 GPT、Llama）。
归一化维度：对 单个样本的所有特征 进行归一化（而非批次维度）。
实现变化：在代码中，仅需将归一化轴从 axis=0（批次维度）改为 axis=1（特征维度）。

# Batch normalization
bnmeani = hpreact.mean(0, keepdim=True)  
bnstdi = hpreact.std(0, keepdim=True)   
# Layer normalization
bnmeani = hpreact.mean(1, keepdim=True)  
bnstdi = hpreact.std(1, keepdim=True)  

2. 实例归一化（Instance Normalization）

对 每个样本的每个通道 独立归一化，常用于风格迁移任务。

3. 组归一化（Group Normalization）

折中方案：将通道分组，对每组内的数据进行归一化。
极端情况：
- 组大小 = 1 → 等同于 InstanceNorm。
- 组大小 = 通道数 → 等同于 LayerNorm。
优点：对批次大小不敏感，适用于小批次训练。,