归一化流

归一化流#

本课程将介绍归一化流，一种用于表示学习的生成模型。虽然不如 VAE、GAN 或扩散模型知名，但它们仍具有多项优势。

GAN 和 VAE 无法精确评估概率分布。GAN 完全无法做到这一点，而 VAE 则使用证据下界（ELBO）近似。这在训练过程中会带来问题：VAE 生成的图像常常模糊，而 GAN 则可能陷入模式崩溃（mode collapse）。

归一化流为这些问题提供了解决方案。

工作原理#

归一化流是由一系列可逆变换（双射）组成的模型。其核心思想是将复杂的数据分布（如图像）通过连续变换，逐步映射为简单的已知分布（如标准正态分布 \(N(0,1)\)）。

训练过程通过最大化数据似然实现，即最小化真实数据概率密度的负对数似然（\(-\log p(x)\)）。通过优化变换参数，使生成分布与目标分布尽可能接近。

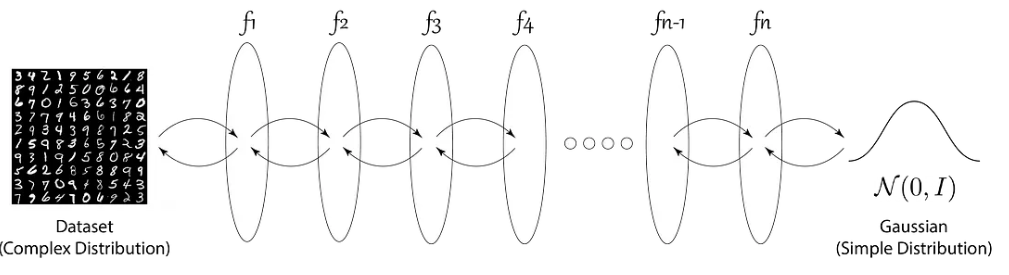归一化流示意图 图片来源：归一化流入门博文

优势与局限#

优势：

  • 训练过程非常稳定，不易发散

  • 比 GAN 或 VAE 更易收敛

  • 生成数据时无需引入噪声

局限：

  • 表达能力不如 GAN 或 VAE 强

  • 由于需满足双射性和体积保持，潜在空间维度高且难以解释

  • 生成结果的质量通常低于 GAN 或 VAE

注：归一化流背后有深刻的理论基础，但本课程不展开详述。如需深入了解，可参考斯坦福大学 CS236 课程的相关笔记。”

Contents