逻辑回归#
人工神经元#
现在进入核心内容:人工神经元!
下图展示了人工神经元的工作原理:
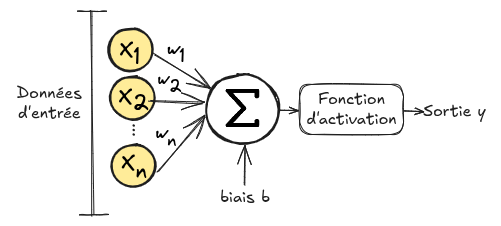
人工神经元接收一个输入向量 \(\mathbf{x}=(x_1, x_2, ..., x_n)\)。向量中的每个元素 \(x_i\) 会乘以一个权重 \(w_i\),然后将所有乘积相加并加上一个偏置 \(b\)。这个总和会经过一个称为激活函数 \(\phi\) 的函数处理。 输出结果为:\(输出 = \phi(\sum_{i=0}^{n} w_i x_i + b)\)。 之所以称为人工神经元,是因为它模仿了生物神经元的工作方式。
激活函数#
Heaviside 阶跃函数: 最早的人工神经元(感知器)使用阈值函数作为激活函数。该函数根据加权和与预定阈值进行决策(输出 0 或 1)。 \(heaviside(x) = \left\{ \begin{array}{ll} 1 & \text{如果 } x > 0 \\ 0 & \text{否则} \end{array} \right. \text{,其中 } x=\sum_{i=0}^{n} w_i x_i + b\) 这种激活函数适用于二分类问题,但不适用于多类别问题。此外,该函数不可导,因此难以使用梯度下降算法来优化神经元的权重 \(w_i\)。
近代的激活函数更适合通过梯度下降训练神经网络。首先,它们是可导的,因此可以应用梯度下降算法。其次,它们是非线性的,使得神经网络能够学习复杂的表示。此外,每种激活函数还有其特定的优势。
其中一种“近代”激活函数是 Sigmoid 函数,我们将在这里详细介绍:
Sigmoid 函数: Sigmoid 函数是一种特别有用的激活函数,因为它的输出可以类比为概率。该函数通过以下公式将输入值转换为 0 到 1 之间的值: \(sigmoid(x) = \frac{1}{1 + e^{-x}} \text{,其中 } x=\sum_{i=0}^{n} w_i x_i + b\)
# Tracé de la fonction sigmoïde
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.linspace(-10, 10, 100)
y = sigmoid(x)
plt.plot(x, y)
plt.title('Fonction sigmoïde')
plt.xlabel('x')
plt.ylabel('sigmoid(x)')
plt.grid(True)
plt.show()
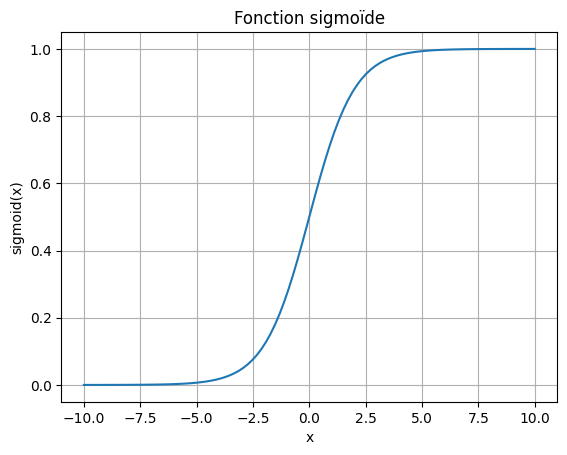
该函数是可导的,其导数为: \(sigmoid'(x) = sigmoid(x) \cdot (1 - sigmoid(x))\) 因此,当使用该激活函数时,我们可以对人工神经元应用梯度下降算法。
还有许多其他激活函数,每种都有其特定用途。我们将在后续课程中介绍它们(如 \(Tanh\)、\(ReLU\)、\(Softmax\))。
应用#
为了更好地理解逻辑回归,我们通过一个具体的例子来学习。
在这个例子中,我们将根据三个信息来判断一名学生是否能被其理想大学录取:入学考试成绩、前一年的平均成绩以及推荐信的质量。
虽然我们不知道学校录取或拒绝学生的具体计算方法,但我们拥有相关的数据和对应的录取决定。
输入信息的取值范围在 0 到 1 之间,1 表示最佳成绩。录取 = 1 表示被录取,录取 = 0 表示被拒绝。
from tabulate import tabulate
# Définition des données d'entraînement
values_train = [[0.7, 0.8, 0.1], [0.4, 0.9, 0.5], [0.2, 0.3, 0.9], [0.9, 0.9, 0.6]]
labels_train = [1, 0, 0, 1]
# Ajout des noms de colonnes
data = [['Examen', 'Moyenne', 'Motivation', 'Admis']]
data.extend([[values_train[i][0], values_train[i][1], values_train[i][2], labels_train[i]] for i in range(len(values_train))])
# Affichage du tableau
print(tabulate(data, headers="firstrow", tablefmt="fancy_grid"))
╒══════════╤═══════════╤══════════════╤═════════╕
│ Examen │ Moyenne │ Motivation │ Admis │
╞══════════╪═══════════╪══════════════╪═════════╡
│ 0.7 │ 0.8 │ 0.1 │ 1 │
├──────────┼───────────┼──────────────┼─────────┤
│ 0.4 │ 0.9 │ 0.5 │ 0 │
├──────────┼───────────┼──────────────┼─────────┤
│ 0.2 │ 0.3 │ 0.9 │ 0 │
├──────────┼───────────┼──────────────┼─────────┤
│ 0.9 │ 0.9 │ 0.6 │ 1 │
╘══════════╧═══════════╧══════════════╧═════════╛
在这个问题中,我们的目标是判断得分为 \([考试=0.8, 平均成绩=0.7, 动机=0.2]\) 和 \([考试=0.4, 平均成绩=0.5, 动机=0.9]\) 的学生是否被录取。
可以看出,\(考试\)、\(平均成绩\) 和 \(动机\) 对应于我们的输入 \(x_i\)。通过逻辑回归,我们的目标是找到与训练数据相符的最优权重 \(w_i\)。
为了简化,我们设定: \(x_0=考试\),\(x_1=平均成绩\),\(x_2=动机\),\(y_{true}=录取\)。
代价函数#
在梯度下降的例子中,我们的目标是找到一个函数的最小值。梯度下降算法在这些场景中表现优异。对于我们的新问题,我们需要找到一个函数,当我们最小化该函数时,可以提高预测的准确性。
在二分类问题中,\(y_{true}\) 的值为 1 表示学生被录取,0 表示未被录取。
我们的目标是预测学生是否被录取,即预测输出 \(pred\)。
在训练过程中,我们希望训练逻辑回归模型,使其预测值 \(pred\) 接近 \(y_{true}\)。
为此,我们使用负对数似然函数,其表达式如下: \(\text{loss} = - \left( y_{\text{true}} \cdot \log(\text{pred}) + (1 - y_{\text{true}}) \cdot \log(1 - \text{pred}) \right)\)
关于逻辑回归和负对数似然损失的更多细节,请参阅此链接。
重要的是理解该函数如何根据我们的预测 \(pred\) 和标签 \(y_{true}\) 变化。
我们以 \(y_{true}=1\) 为例,分析两种情况:
如果 \(pred=0.9\),即模型预测学生有 90% 的概率被录取(一个好的预测),那么: \(\text{loss} = - \left( 1.0 \cdot \log(0.9) + (1 - 1.0) \cdot \log(1 - 0.9) \right)\) \(\text{loss} = - \left( 1.0 \cdot \log(0.9) + 0 \cdot \log(0.1) \right)\) \(\text{loss} = - \left( 1.0 \cdot \log(0.9) \right)\) \(\text{loss} = 0.046\) 损失值较小,说明这是一个好的预测。
如果 \(pred=0.2\),即模型预测学生只有 20% 的概率被录取(一个不好的预测),那么: \(\text{loss} = - \left( 1.0 \cdot \log(0.2) + (1 - 1.0) \cdot \log(1 - 0.2) \right)\) \(\text{loss} = - \left( 1.0 \cdot \log(0.2) + 0 \cdot \log(0.8) \right)\) \(\text{loss} = - \left( 1.0 \cdot \log(0.2) \right)\) \(\text{loss} = 0.70\) 损失值较大,说明这是一个不好的预测。
对于 \(y_{true}=0\) 的情况,当 \(pred\) 接近 0 时损失值较小,当 \(pred\) 接近 1 时损失值较大(可自行计算验证)。
导数计算#
现在我们有一个需要最小化的函数,因此需要计算该函数关于每个权重 \(w_0\)、\(w_1\)、\(w_2\) 和偏置 \(b\) 的导数。
因此,我们需要计算 \(\frac{\partial loss}{\partial w_0}\)、\(\frac{\partial loss}{\partial w_1}\)、\(\frac{\partial loss}{\partial w_2}\) 和 \(\frac{\partial loss}{\partial b}\)。
对于权重 \(w_0\)、\(w_1\) 和 \(w_2\),导数的计算方式是相同的。
使用链式法则,对于 \(w_0\),我们有: \(\frac{\partial loss}{\partial w_0} = \frac{\partial loss}{\partial pred} \cdot \frac{\partial pred}{\partial w_0}\)
需要注意的是,我们的预测 \(pred\) 是逻辑回归的输出,使用 Sigmoid 激活函数。
对于第一项,损失关于 \(pred\) 的导数为: \(\frac{\partial loss}{\partial pred} = -(\frac{y_{true}}{pred} - \frac{1-y_{true}}{1-pred})\) 这里不详细展开计算过程,但你可以自行验证。
对于第二项,\(pred\) 关于 \(w_0\) 的导数为: \(\frac{\partial pred}{\partial w_0} = pred \cdot (1-pred) \cdot x_0\)
结合这两项,我们得到: \(\frac{\partial loss}{\partial w_0} = -(\frac{y_{true}}{pred} - \frac{1-y_{true}}{1-pred}) \cdot pred \cdot (1-pred) \cdot x_0\)
经过简化(魔法般的简化),得到: \(\frac{\partial loss}{\partial w_0} = (pred-y_{true}) \cdot x_0\)
不详细展开计算,我们同样可以得到: \(\frac{\partial loss}{\partial b} = pred-y_{true}\)
逻辑回归#
现在我们已经具备了所有必要的元素, 我们可以用 Python 定义逻辑回归函数:
# Notre classe de regression logistique
class logistic_regression():
def __init__(self) -> None:
self.w0=np.random.randn()
self.w1=np.random.randn()
self.w2=np.random.randn()
self.b=0
def __call__(self,x0,x1,x2):
# Somme pondérée et ajout du biais
pond=self.w0*x0+self.w1*x1+self.w2*x2+self.b
# Application de la sigmoïde
pred=sigmoid(pond)
return pred
def loss(y_true, y_pred):
# Calcul du loss (log vraisemblance négative)
loss = - (y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))
return loss
def update_weights(model,pred, x0, x1, x2, y_true, learning_rate):
# On calcule les dérivées en fonction des poids et du biais
dL_dw0 = (pred - y_true) * x0
dL_dw1 = (pred - y_true) * x1
dL_dw2 = (pred - y_true) * x2
dL_db = pred - y_true
# On modifie les paramètres pour réduire le loss
# La modification des poids dépend du learning rate, du signe de la dérivée et de la valeur de la dérivée
model.w0 -= learning_rate * dL_dw0
model.w1 -= learning_rate * dL_dw1
model.w2 -= learning_rate * dL_dw2
model.b -= learning_rate * dL_db
# Initialisation du modèle et des hyperparamètres
learning_rate = 0.01
epochs = 1000 # le nombre d'itérations d'entrainement
model = logistic_regression()
在训练模型之前,我们先测试一下对两名学生录取结果的预测。
values_test=[[0.8,0.7,0.7],[0.4,0.5,0.9]]
for value in values_test:
x0,x1,x2=value
pred = model(x0, x1, x2)
print("L'élève avec Examen = "+str(x0)+ ", Moyenne = "+str(x1)+" et Motivation = "+str(x2)+ " a "+str(round(pred*100)) + "% de chance d'être admis")
L'élève avec Examen = 0.8, Moyenne = 0.7 et Motivation = 0.7 a 60% de chance d'être admis
L'élève avec Examen = 0.4, Moyenne = 0.5 et Motivation = 0.9 a 59% de chance d'être admis
可以看到模型非常不确定,给出的概率是随机的,这是因为模型的权重是随机初始化的。
现在,我们在训练数据上训练模型。
# Entraînement
for epoch in range(epochs):
# Mise à jour des poids pour chaque exemple
total_loss = 0
for (x0, x1, x2), y_true in zip(values_train, labels_train):
pred = model(x0, x1, x2)
update_weights(model,pred, x0, x1, x2, y_true, learning_rate)
total_loss += loss(y_true, pred)
avg_loss = total_loss / len(labels_train)
# Affichage de la perte pour suivre la progression de l'entraînement
if ((epoch + 1) % 5000 == 0) or (epoch==0):
print(f"Epoch {epoch + 1}/{epochs}, Loss: {avg_loss}")
Epoch 1/40000, Loss: 0.01468091027998586
Epoch 5000/40000, Loss: 0.013032955086147595
Epoch 10000/40000, Loss: 0.011715352279809266
Epoch 15000/40000, Loss: 0.010638348324912276
Epoch 20000/40000, Loss: 0.009741762611763436
Epoch 25000/40000, Loss: 0.008983896958517028
Epoch 30000/40000, Loss: 0.008334957514714105
Epoch 35000/40000, Loss: 0.007773096000082178
Epoch 40000/40000, Loss: 0.007281930357182074
print(model.w0, model.w1, model.w2, model.b)
for value in values_test:
x0,x1,x2=value
pred = model(x0, x1, x2)
print("L'élève avec Examen = "+str(x0)+ ", Moyenne = "+str(x1)+" et Motivation = "+str(x2)+ " a "+str(round(pred*100)) + "% de chance d'être admis")
19.464301071981186 -3.27230109363944 -8.244865180820856 -4.903197398150705
L'élève avec Examen = 0.8, Moyenne = 0.7 et Motivation = 0.7 a 93% de chance d'être admis
L'élève avec Examen = 0.4, Moyenne = 0.5 et Motivation = 0.9 a 0% de chance d'être admis
可以看到,现在我们的模型对其预测更加自信,并且给出了与训练数据相符的预测结果。