导数与梯度下降

导数与梯度下降#

这门课程介绍了梯度下降算法，这是深度学习的基石。为了更好地理解它，让我们回顾一下导数的概念。

import matplotlib.pyplot as plt 
import numpy as np

导数的直观理解#

让我们考虑一个函数：\(f(x) = 2x^2 - 3x + 4\)

def f(x):
  return 2*x**2-3*x+4
f(3)

13

让我们使用 matplotlib 绘制这个函数。

xs = np.arange(-5, 5, 0.25)
ys = f(xs)
plt.plot(xs, ys)

[<matplotlib.lines.Line2D at 0x7ae9dcdf63d0>]
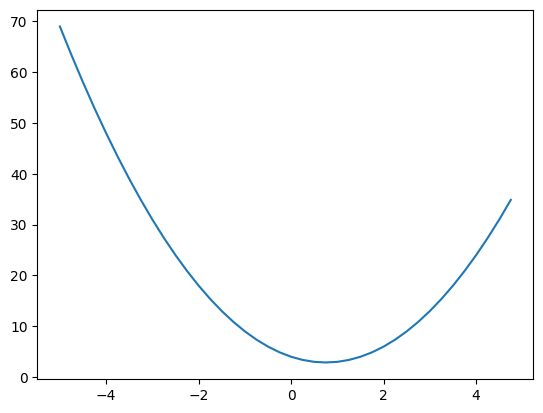
../_images/8ae53ec1c1a7a83c40158a7e0d6aeac20e0c0089b96c23bc11822f2fad3e62d5.png

导数给出了曲线在某一点的切线斜率。 为了计算它，我们使用以下公式： \(f'(x) = \lim_{h \to 0} \frac{f(x+h)-h}{h}\) 当 \(h\) 很小时，我们可以数值估计斜率。

注：斜率显示了 \(x\) 变化时 \(y\) 的变化情况。如果 \(x\) 增加 1，而 \(y\) 增加 2，那么斜率为 2。

h=0.0001
x=-1.0
print("Dérivée en x=-1 : ", (f(x+h)-f(x))/h)
x=2.0
print("Dérivée en x=2 : ", (f(x+h)-f(x))/h)

Dérivée en x=-1 :  -6.999800000002665
Dérivée en x=2 :  5.000200000004895

图表显示在 \(x=-1\) 时斜率为负，在 \(x=2\) 时斜率为正。 导数的 符号 表示斜率的方向，其 值 表示斜率的强度。 让我们参考 常见导数 验证： 对于 \(f(x)=2x²-3x+4\)，我们有 \(f'(x)=4x-3\)。 我们发现 \(f'(-1) \approx -7\) 和 \(f'(2) \approx 5\)。 结果不精确，因为 \(h\) 不是无限小。

# On définit deriv_f = f'(x)
def deriv_f(x):
  return 4*x-3

梯度下降的优化基础#

优化旨在最小化或最大化目标函数。 为了找到最小值，有两种方法：

  1. 解 \(f'(x)=0\)： \(4x-3=0 \implies x=\frac{3}{4}\)。 这在本例中给出了最小值，但并非总是如此。

  2. 使用 梯度下降： 从一个点开始，例如 \(x=2\)。 计算 \(f'(2)=5\)。正斜率意味着如果 \(x\) 增加，\(f(x)\) 也会增加，反之亦然。 为了最小化 \(f(x)\)，调整 \(x\) 使用一个因子 \(\alpha\)（学习率）。 我们得到 \(x_{new}=x - slope \times \alpha=2-0.5=1.5\)。 重新计算 \(f'(1.5)=3\)，仍然为正，因此我们进一步减小 \(x\)。 梯度下降在循环中调整 \(x\)，直到达到最小值，考虑斜率。

# Descente du gradient
x=2.0 # valeur aléatoire de x
alpha=0.01 # pas
iterations=250 # nombre d'itérations

for i in range(iterations):
  grad=deriv_f(x)
  if (grad>0):
    x=x-alpha
  elif(grad<0):
    x=x+alpha
  else:
    print("minimum found YAY, x = ",x)
print("approximate minimum found YAY, x = ",x)

approximate minimum found YAY, x =  0.7599999999999989

我们得到 \(x \approx \frac{3}{4}\)。使用更小的步长（\(\alpha\)）和更多的迭代次数，我们可以精细化结果。

链式法则#

在继续之前，让我们回顾一下深度学习的一个关键数学规则：链式法则。 它允许我们训练网络隐藏层的参数。 如果 \(y\) 依赖于 \(u\)，而 \(u\) 又依赖于 \(x\)，那么： \(\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}\)

让我们以依赖函数为例： \(u=2x²-x-2\) \(y=3u+1\) \(\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}\)，其中 \(\frac{dy}{du}=3\) 和 \(\frac{du}{dx}=2x-1\) \(\frac{dy}{dx}=3(2x-1) = 6x-3\) 现在，我们知道 \(x\) 如何影响 \(y\)，并且可以应用梯度下降算法。

x=2.0
def deriv_y_x(x):
  return 6*x-3
for i in range(iterations):
  grad=deriv_y_x(x)
  if (grad>0):
    x=x-alpha
  elif(grad<0):
    x=x+alpha
  else:
    print("minimum found YAY, x = ",x)
print("approximate minimum found YAY, x = ",x)

approximate minimum found YAY, x =  0.49999999999999867

多变量优化#

到目前为止，我们一直在寻找单变量 \(x\) 的函数的最小值。 优化方法的一个优势是，我们可以同时使用梯度下降优化多个变量。为此，我们需要计算每个变量的导数。

让我们在模型中取 3 个变量 \(a\)，\(b\)，和 \(c\)： \(u=3a²-2a+b²+1\) \(y=2u+c\) 为了应用梯度下降，让我们计算 \(\frac{dy}{da}\)，\(\frac{dy}{db}\)，和 \(\frac{dy}{dc}\)。 使用链式法则：

  • 对于 \(a\)： \(\frac{dy}{da} = \frac{dy}{du}\cdot\frac{du}{da} = 2(6a-2) = 12a-4\)

  • 对于 \(b\)： \(\frac{dy}{db} = \frac{dy}{du}\cdot\frac{du}{db} = 2(2b) = 4b\)

  • 对于 \(c\)： \(\frac{dy}{dc}=1\) 现在，我们可以应用梯度下降。

def deriv_y_a(a):
  return 12*a-4
def deriv_y_b(b):
  return 4*b
def deriv_y_c(c):
  return 1

a=1.0
b=1.0
c=1.0
alpha=0.05
def deriv_y_x(x):
  return 6*x-3
for i in range(iterations):
  grad_a=deriv_y_a(a)
  grad_b=deriv_y_b(b)
  grad_c=deriv_y_c(b)
  if (grad_a>0):
    a=a-alpha
  else:
    a=a+alpha
  if (grad_b>0):
    b=b-alpha
  else:
    b=b+alpha
  if (grad_c>0):
    c=c-alpha
  else:
    c=c+alpha
print("approximate minimum found YAY, a = "+str(a)+" b = "+str(b)+" c = "+str(c))

approximate minimum found YAY, a = 0.29999999999999966 b = -3.191891195797325e-16 c = -11.50000000000003

我们已经找到了使 \(y\) 最小化的值：

  • \(c\) 在许多迭代后趋向于负无穷。

  • \(b\) 等于 0。

  • \(a\) 等于 0.3。

Contents