变分自编码器#
本课程将介绍变分自编码器(Variational Autoencoders, VAE)。我们将从自编码器课程的简要回顾开始,然后介绍如何将 VAE 作为生成模型使用。本课程内容参考了这篇博客文章,并未深入探讨 VAE 的数学细节。 本笔记本中的图示同样来自该博客文章。
自编码器回顾#
自编码器是一种沙漏形的神经网络。它由两部分组成:
编码器:将输入数据压缩到一个低维的潜在空间
解码器:从潜在空间的表示中重构原始数据
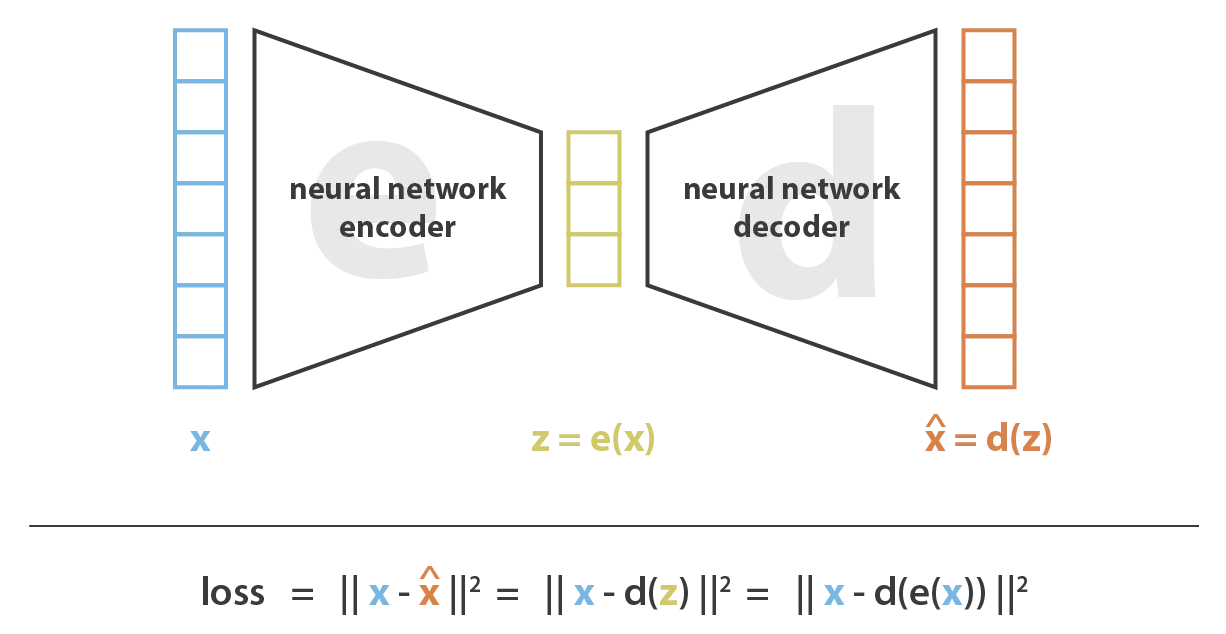
自编码器有多种应用,但其核心功能是数据压缩。它通过梯度下降优化实现数据的高效压缩。
直观理解#
假设解码器的潜在空间是规则的(即服从已知的概率分布),那么我们可以从该分布中随机采样一个元素来生成新数据。然而,在传统自编码器中,潜在空间通常不规则,因此无法用于数据生成。
这是因为自编码器的损失函数仅关注重构质量,而不约束潜在空间的结构。
因此,我们需要强制自编码器的潜在空间具有特定结构,以便能够从中生成新数据。
变分自编码器#
变分自编码器(VAE)是一种约束潜在空间结构的自编码器,使其能够用于数据生成。其训练过程经过特殊调整以实现这一目标。
与传统自编码器不同,VAE 的编码器将输入数据编码为一个概率分布(而非单一值),具体来说,是预测一个正态分布的两个参数:
均值 \(\mu\)
方差 \(\sigma^2\)
VAE 的训练流程如下:
编码器将输入数据编码为概率分布(预测 \(\mu\) 和 \(\sigma^2\))
从该高斯分布中随机采样一个值
解码器根据采样值重构数据
通过反向传播更新网络权重
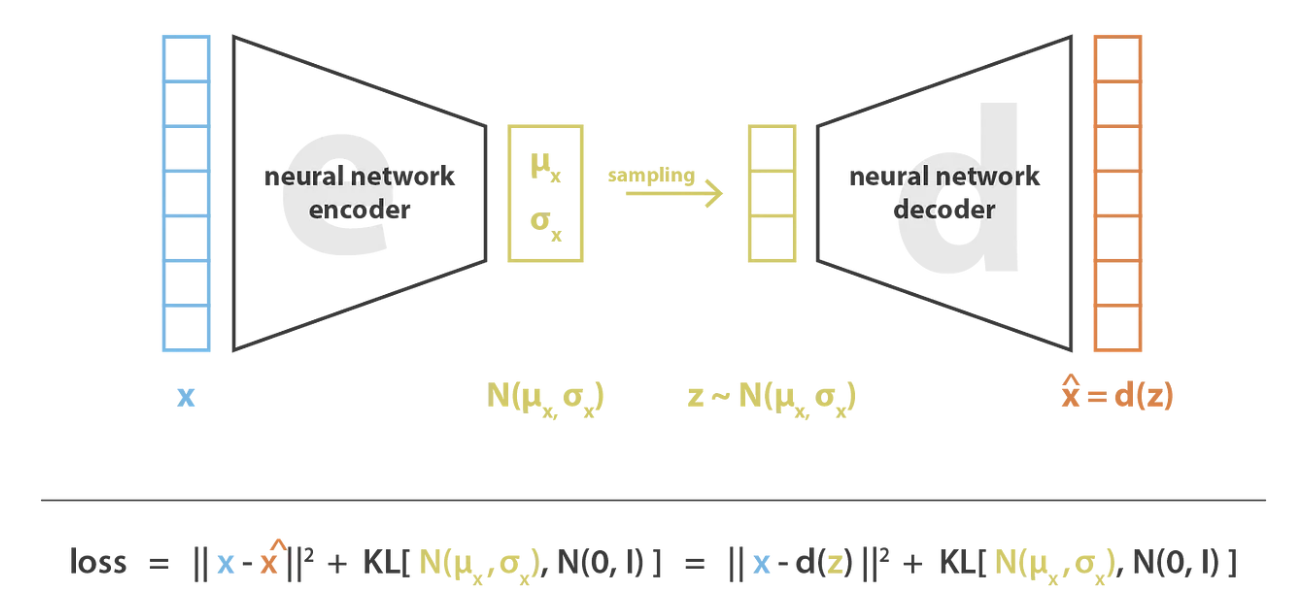
为了确保训练符合预期,我们需要在损失函数中添加一个Kullback-Leibler 散度(KL 散度)项。该项能够推动潜在空间的分布接近标准正态分布(均值为 0,方差为 1)。
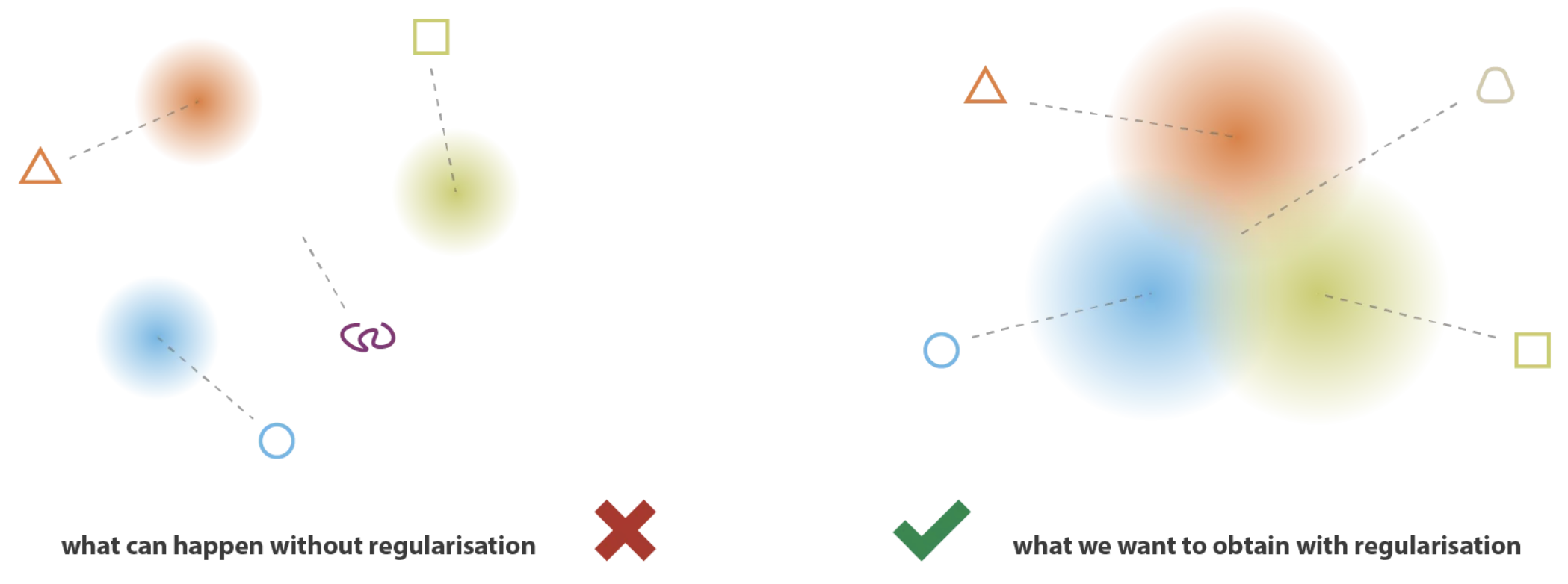
为了生成一致性数据,需要满足两个关键性质:
连续性:潜在空间中相近的点,在输出空间中应生成相似的数据
完备性:解码后的数据在输出空间中应具有实际意义
KL 散度能够保证上述两个性质:
若仅使用重构损失,VAE 可能退化为传统自编码器(预测接近 0 的方差,相当于单点预测)
KL 散度能够鼓励潜在空间中的分布相互接近,从而确保采样生成的数据始终保持一致性
注:变分自编码器背后有重要的理论基础,但本课程不做深入探讨。如需了解更多细节,可参考斯坦福大学 CS236 课程,特别是此链接的内容。