Métriques d’évaluation des modèles#
L’évaluation est une étape clé dans l’entraînement d’un modèle. Jusqu’à présent, on a surtout utilisé le loss de test ou des métriques basiques comme la précision. Selon le problème à résoudre, différentes métriques permettent d’évaluer divers aspects du modèle. Ce cours en présente plusieurs, à utiliser selon les besoins.
Métriques pour la classification#
Matrice de confusion#
En classification binaire, on peut visualiser les prédictions du modèle ainsi :
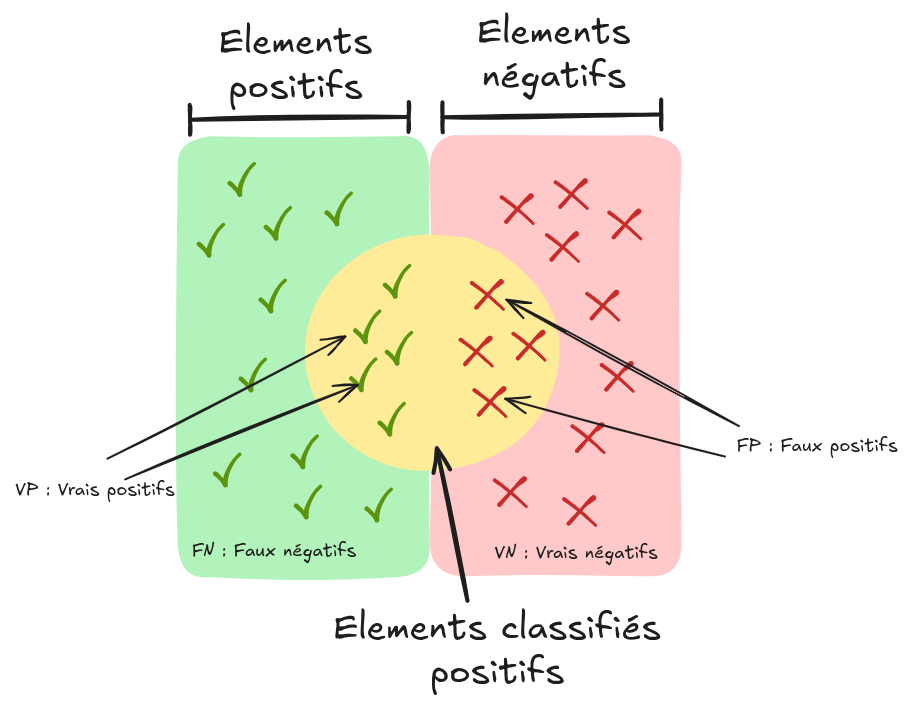
Source : Wikipedia
Voici les termes de base :
Faux positif (fp) : Élément classé positif alors qu’il est négatif.
Vrai positif (vp) : Élément classé positif et effectivement positif.
Faux négatif (fn) : Élément classé négatif alors qu’il est positif.
Vrai négatif (vn) : Élément classé négatif et effectivement négatif.
On peut représenter ces concepts dans une matrice de confusion :
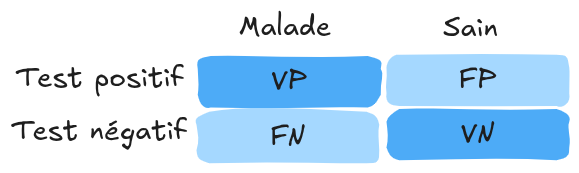
Note : Pour une classification multi-classes, la matrice de confusion aide à identifier les confusions entre classes.
Précision, rappel et spécificité#
À partir de la matrice de confusion, on peut calculer plusieurs métriques :
Précision : \(Précision=\frac{vp}{vp+fp}\). Proportion d’éléments positifs correctement classifiés parmi tous ceux classés positifs.
Rappel (ou sensibilité) : \(Rappel=\frac{vp}{vp+fn}\). Proportion d’éléments positifs correctement classifiés parmi tous les éléments positifs.
Spécificité (ou sélectivité) : \(Spécificité=\frac{vn}{vn+fp}\). Proportion d’éléments négatifs correctement classifiés parmi tous les éléments négatifs.
Accuracy#
L’accuracy (attention, ne pas confondre avec la précision) mesure le nombre de prédictions correctes sur le total des prédictions. Sa formule est : \(Accuracy=\frac{vp+vn}{vp+vn+fp+fn}\)
Note : À utiliser avec prudence en cas de déséquilibre de classes (class imbalance).
F1-score#
Le F1-score est une métrique couramment utilisée. Il s’agit de la moyenne harmonique entre précision et rappel : \(F1=2 \times \frac{précision \times rappel}{précision + rappel}\)
Si précision et rappel sont proches, le F1-score est proche de leur moyenne.
Courbe ROC#
La courbe ROC (Receiver Operating Characteristic) montre les performances d’un modèle de classification binaire à différents seuils. Elle comprend :
Axe des X : Taux de faux positifs (\(1-spécificité\)). Proportion d’éléments négatifs mal classés en positifs.
Axe des Y : Taux de vrais positifs (\(rappel\)). Proportion d’éléments positifs bien classés.
Chaque point de la courbe correspond à un seuil de décision différent.
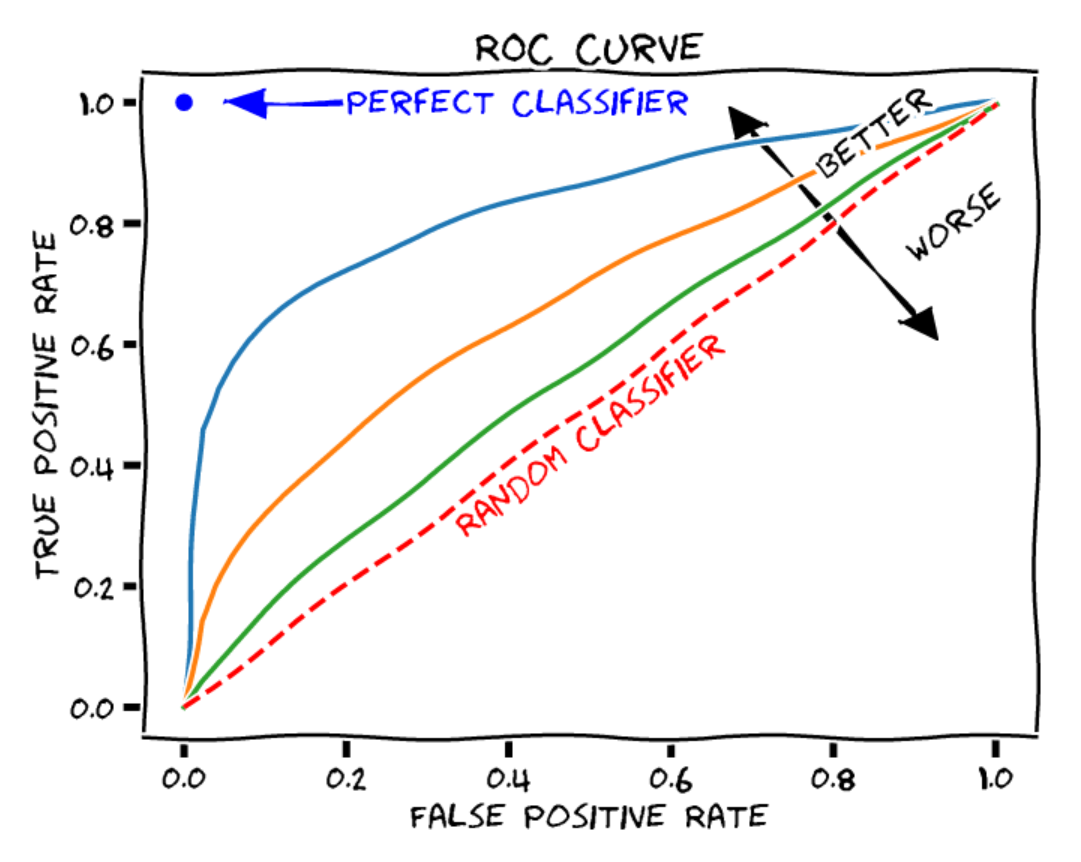
Source : Blogpost
Pour évaluer un modèle, on calcule l’aire sous la courbe (AUROC) :
Classifieur aléatoire : AUROC = 0.5
Classifieur parfait : AUROC = 1
Log loss#
On peut simplement utiliser la valeur du loss sur les données de test comme métrique. Comme le loss reflète l’objectif, cela peut suffire dans beaucoup de cas.
Métriques pour la régression et les autoencodeurs#
Mean Absolute Error (MAE)#
Pour les modèles de régression ou les autoencodeurs, on compare les prédictions aux valeurs réelles en calculant une distance. La MAE (Mean Absolute Error) est la moyenne des erreurs absolues : \(\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} \left| y_i - \hat{y}_i \right|\)
Mean Squared Error (MSE)#
On utilise souvent le MSE (Mean Squared Error), qui est la moyenne des carrés des erreurs : \(\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} \left( y_i - \hat{y}_i \right)^2\)
Métriques pour la détection et la segmentation#
AP et mAP#
En détection, on ne peut pas juste évaluer la précision. Il faut considérer différents seuils de rappel pour une évaluation pertinente. L’average precision (AP) se calcule ainsi :
\(\text{AP} = \int_{0}^{1} \text{Precision}(r) \, \text{d}r\)
Ou de manière discrète :
\(\text{AP} = \sum_{k=1}^{K} \text{Precision}(r_k) \cdot (r_k - r_{k-1})\)
Où :
\(\text{Precision}(r)\) : Précision au rappel \(r\)
\(K\) : Nombre de points d’évaluation du rappel
\(r_k\) et \(r_{k-1}\) : Rappels aux points \(k\) et \(k-1\)
La mean average precision (mAP) est la moyenne des AP pour toutes les classes dans un problème de détection multi-classes. Elle donne une évaluation globale du modèle en tenant compte de toutes les classes.
\(\text{mAP} = \frac{1}{C} \sum_{c=1}^{C} \text{AP}_c\)
Intersection Over Union (IoU)#
En détection et segmentation, l’IoU (Intersection Over Union) est une métrique clé. En détection, on fixe un seuil d’IoU en dessous duquel une détection est considérée comme invalide (non comptée pour le mAP). En segmentation, l’IoU évalue directement la qualité.
\(\text{IoU} = \frac{|\text{Intersection}|}{|\text{Union}|} = \frac{|\text{Prédiction} \cap \text{Vérité terrain}|}{|\text{Prédiction} \cup \text{Vérité terrain}|}\)
Note : L’IoU pénalise les petits objets et classes rares. Pour réduire ce biais, on peut utiliser le dice coefficient.
Dice Coefficient#
En segmentation, on utilise souvent le dice coefficient plutôt que l’IoU. Sa formule est :
\(\text{Dice} = \frac{2 \times |\text{Prédiction} \cap \text{Vérité terrain}|}{|\text{Prédiction}| + |\text{Vérité terrain}|}\)
Le dice coefficient met l’accent sur l’intersection entre prédiction et vérité terrain, en donnant plus de poids aux éléments communs.
Évaluation des modèles de langage#
Évaluer les modèles de langage est complexe. Bien qu’on puisse utiliser le loss de test, cela ne donne pas une idée précise des performances réelles. Plusieurs méthodes et benchmarks existent pour évaluer ces modèles selon différents critères.
Sources :
Évaluation des modèles de génération d’images#
Évaluer les modèles de génération d’images est complexe. On a souvent besoin d’une évaluation humaine pour juger de la qualité des images générées.