Implémentation du Vision Transformer

Dans ce notebook, on va implémenter le Vision Transformer et le tester sur le petit dataset CIFAR-10. L’implémentation reprend des éléments du notebook 2 “GptFromScratch”, donc il est nécessaire de les faire dans l’ordre.

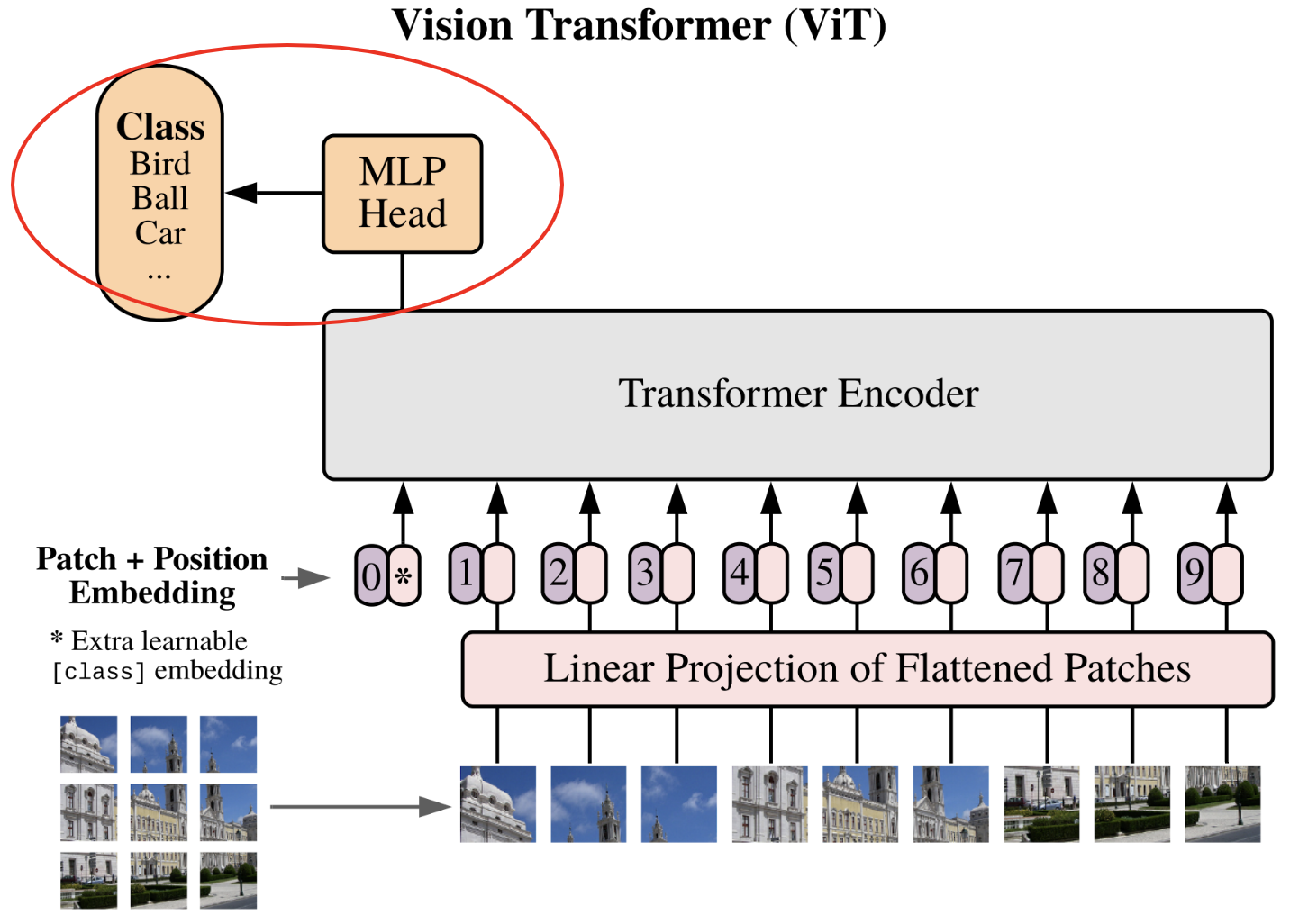
On se base sur l’article An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale.

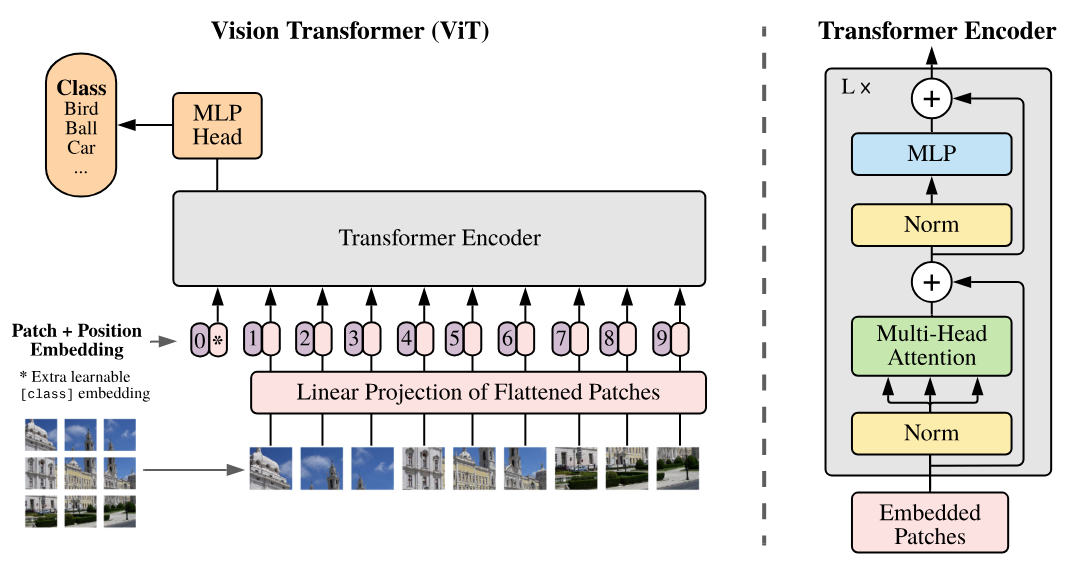
Voici la figure importante de cet article qu’on va implémenter petit à petit :

import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision.transforms as T
import torchvision.datasets as datasets
import matplotlib.pyplot as plt

# Detection automatique du GPU
device = "cpu"
if torch.cuda.is_available():
    device = "cuda"
print(f"using device: {device}")

using device: cpu

Reprise du code précédent

On va d’abord reprendre le code du notebook 2 de ce cours en y apportant quelques modifications.

Couche de self-attention

Si vous vous en souvenez, dans le notebook 2, on a implémenté la couche masked multi-head attention pour entraîner un transformer de type decoder. Pour les images, on veut un transformer de type encoder, donc il faut changer notre implémentation.

C’est assez simple : on avait une multiplication par une matrice triangulaire inférieure pour masquer le “futur” dans le decoder. Mais dans l’encoder, on ne veut pas masquer le futur, donc il suffit de supprimer cette multiplication par la matrice.

Voici le code Python ajusté :

class Head_enc(nn.Module):
    """ Couche de self-attention unique """

    def __init__(self, head_size,n_embd,dropout=0.2):
        super().__init__()
        self.key = nn.Linear(n_embd, head_size, bias=False)
        self.query = nn.Linear(n_embd, head_size, bias=False)
        self.value = nn.Linear(n_embd, head_size, bias=False)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        B,T,C = x.shape
        k = self.key(x)   # (B,T,C)
        q = self.query(x) # (B,T,C)
        # Le * C**-0.5 correspond à la normalisation par la racine de head_size
        wei = q @ k.transpose(-2,-1) * C**-0.5 # (B, T, C) @ (B, C, T) -> (B, T, T)
        # On a supprimer le masquage du futur
        wei = F.softmax(wei, dim=-1) # (B, T, T)
        wei = self.dropout(wei)
        v = self.value(x) # (B,T,C)
        out = wei @ v # (B, T, T) @ (B, T, C) -> (B, T, C)
        return out

Multi-head self-attention

Pour avoir plusieurs head, on va simplement reprendre notre classe du notebook 2 mais en utilisant Head_enc au lieu de Head :

class MultiHeadAttention(nn.Module):
    """ Plusieurs couches de self attention en parallèle"""

    def __init__(self, num_heads, head_size,n_embd,dropout):
        super().__init__()
        # Création de num_head couches head_enc de taille head_size
        self.heads = nn.ModuleList([Head_enc(head_size,n_embd,dropout) for _ in range(num_heads)])
        self.proj = nn.Linear(n_embd, n_embd)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        out = torch.cat([h(x) for h in self.heads], dim=-1)
        out = self.dropout(self.proj(out))
        return out

Feed forward layer

On réutilise aussi notre implémentation de la feed forward layer, on change juste la fonction d’activation ReLU en GeLU comme décrit dans l’article :

class FeedFoward(nn.Module):

    def __init__(self, n_embd,dropout):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(n_embd, 4 * n_embd),
            nn.GELU(),
            nn.Linear(4 * n_embd, n_embd),
            nn.Dropout(dropout),
        )

    def forward(self, x):
        return self.net(x)

Transformer encoder block

Et enfin, on peut construire notre block de transformer encoder correspondant à celui qu’on voit sur la figure plus haut :

class TransformerBlock(nn.Module):
    """ Block transformer"""

    def __init__(self, n_embd, n_head,dropout=0.):
        super().__init__()
        head_size = n_embd // n_head
        self.sa = MultiHeadAttention(n_head, head_size,n_embd,dropout)
        self.ffwd = FeedFoward(n_embd,dropout)
        self.ln1 = nn.LayerNorm(n_embd)
        self.ln2 = nn.LayerNorm(n_embd)

    def forward(self, x):
        x = x + self.sa(self.ln1(x))
        x = x + self.ffwd(self.ln2(x))
        return x

Note : Ici, je suis allé vite sur ces couches car elles ont été implémentées en détail dans le notebook 2. Je vous invite à vous y référer en cas d’incompréhension.

Implémentation du réseau

On va maintenant faire l’implémentation du réseau pas à pas.

Séparation de l’image en patch

La première étape décrite dans l’article est la division de l’image en patchs :

Chaque image est découpée en \(N\) patchs de taille \(p \times p\), puis les patchs sont aplatis (flatten). On passe d’une dimension de l’image \(\mathbf{x} \in \mathbb{R}^{H \times W \times C}\) à une séquence de patchs \(\mathbf{x}_p \in \mathbb{R}^{N \times (P^2 \cdot C)}\).

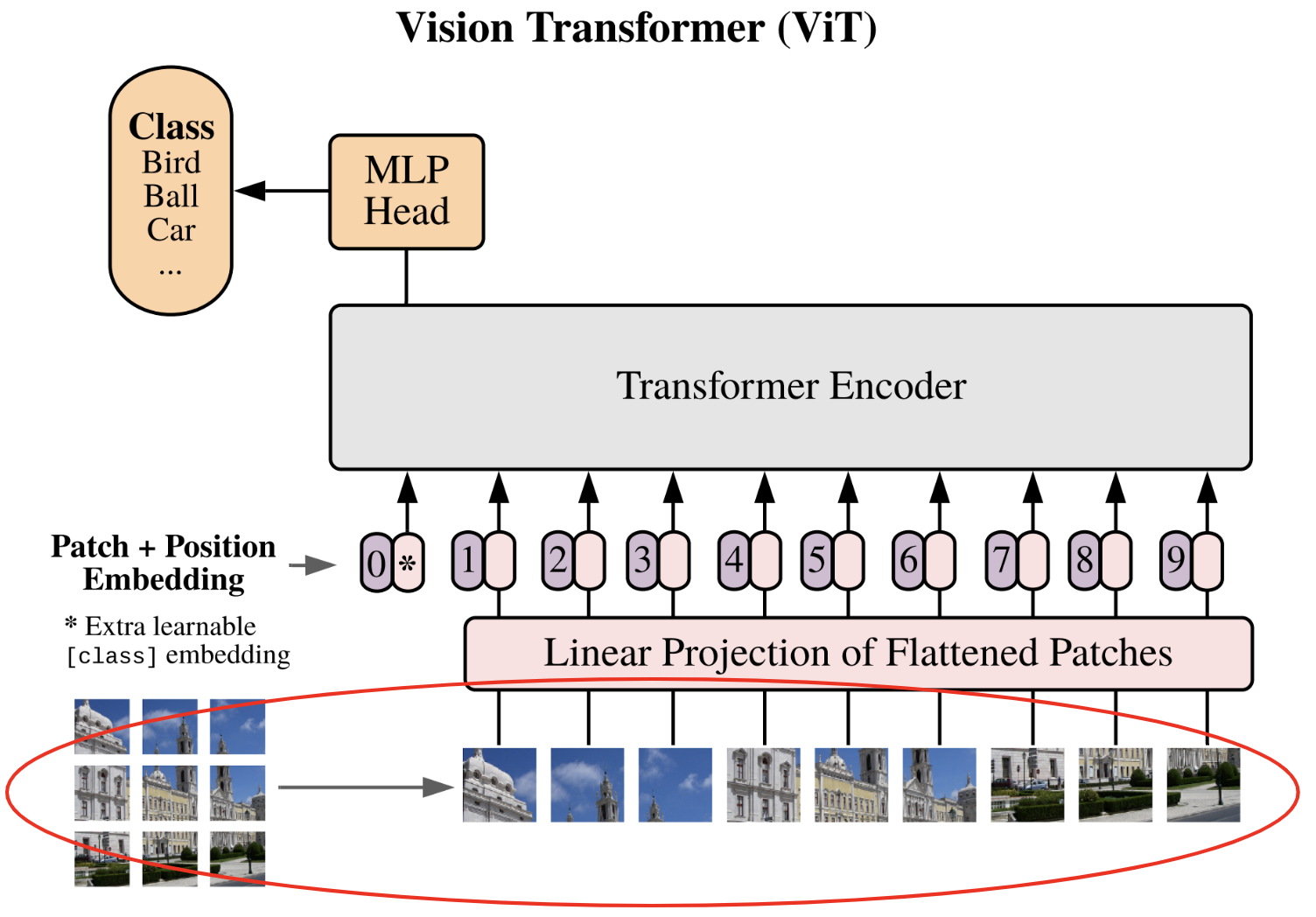
Pour réaliser cela, on va récupérer une image du dataset CIFAR-10 comme exemple, ce qui nous permettra de visualiser si notre code fonctionne.

transform=T.ToTensor() # Pour convertir les éléments en tensor torch directement
dataset = datasets.CIFAR10(root='./../data', train=True, download=True,transform=transform)

Files already downloaded and verified

Récupérons une simple image de ce dataset pour faire nos tests :

image=dataset[0][0]
print(image.shape)
plt.imshow(dataset[0][0].permute(1,2,0).numpy())
plt.axis("off")
plt.show()

torch.Size([3, 32, 32])

Une magnifique grenouille !

Pour choisir la dimension d’un patch, il faut prendre une dimension divisible par 32. Prenons par exemple \(8 \times 8\), ce qui nous fera 16 patchs. Laissons cette valeur comme étant un paramètre qu’on peut choisir.

Dans un premier temps, on peut penser qu’il faut faire deux boucles sur la largeur et la hauteur en récupérant un patch à chaque fois de cette manière :

patch_size = 8
list_of_patches = []
for i in range(0,image.shape[1],patch_size):
    for j in range(0,image.shape[2],patch_size):
        patch=image[:,i:i+patch_size,j:j+patch_size]
        list_of_patches.append(patch)
tensor_patches = torch.stack(list_of_patches)
print(tensor_patches.shape)

torch.Size([16, 3, 8, 8])

Ce n’est pas du tout efficace en termes de code. Avec PyTorch, on peut en fait faire beaucoup plus simplement avec view() et unfold(). Cette étape est un peu compliquée mais nécessaire pour des raisons de continuité en mémoire pour que la fonction view() fonctionne correctement. Faire simplement patches = image.view(-1, C, patch_size, patch_size) ne fonctionnerait pas (vous pouvez essayer pour vous en assurer).

C,H,W = image.shape
# On utilise la fonction unfold pour découper l'image en patch contigus
# Le premier unfold découpe la première dimension (H) en ligne
# Le deuxième unfold découpe chacune des lignes en patch_size colonnes 
# Ce qui donne une image de taille (C, H//patch_size, W//patch_size,patch_size, patch_size)
patches = image.unfold(1, patch_size, patch_size).unfold(2, patch_size, patch_size)
# Permute pour avoir les dimensions dans le bon ordre
patches = patches.permute(1, 2, 0, 3, 4).contiguous()
patches = patches.view(-1, C, patch_size, patch_size)
print(patches.shape)
# On peut vérifier que ça fait bien la même chose
print((patches==tensor_patches).all())

torch.Size([16, 3, 8, 8])
tensor(True)

Maintenant, on va aplatir nos patchs pour avoir notre résultat final.

nb_patches = patches.shape[0]
print(nb_patches)
patches_flat = patches.flatten(1, 3)
print(patches_flat.shape)

16
torch.Size([16, 192])

Définissons une fonction pour faire ces transformations :

# La fonction a été modifiée pour prendre en compte le batch
def image_to_patches(image, patch_size):
    # On rajoute une dimension pour le batch
    B,C,_,_ = image.shape
    patches = image.unfold(2, patch_size, patch_size).unfold(3, patch_size, patch_size)
    patches = patches.permute(0,2, 3, 1, 4, 5).contiguous()
    patches = patches.view(B,-1, C, patch_size, patch_size)
    patches_flat = patches.flatten(2, 4)
    return patches_flat

Nous y sommes ! La première étape est terminée :)

Projection linéaire des patchs

Il est temps de passer à la deuxième étape, qui est la projection linéaire des patchs dans un espace latent.

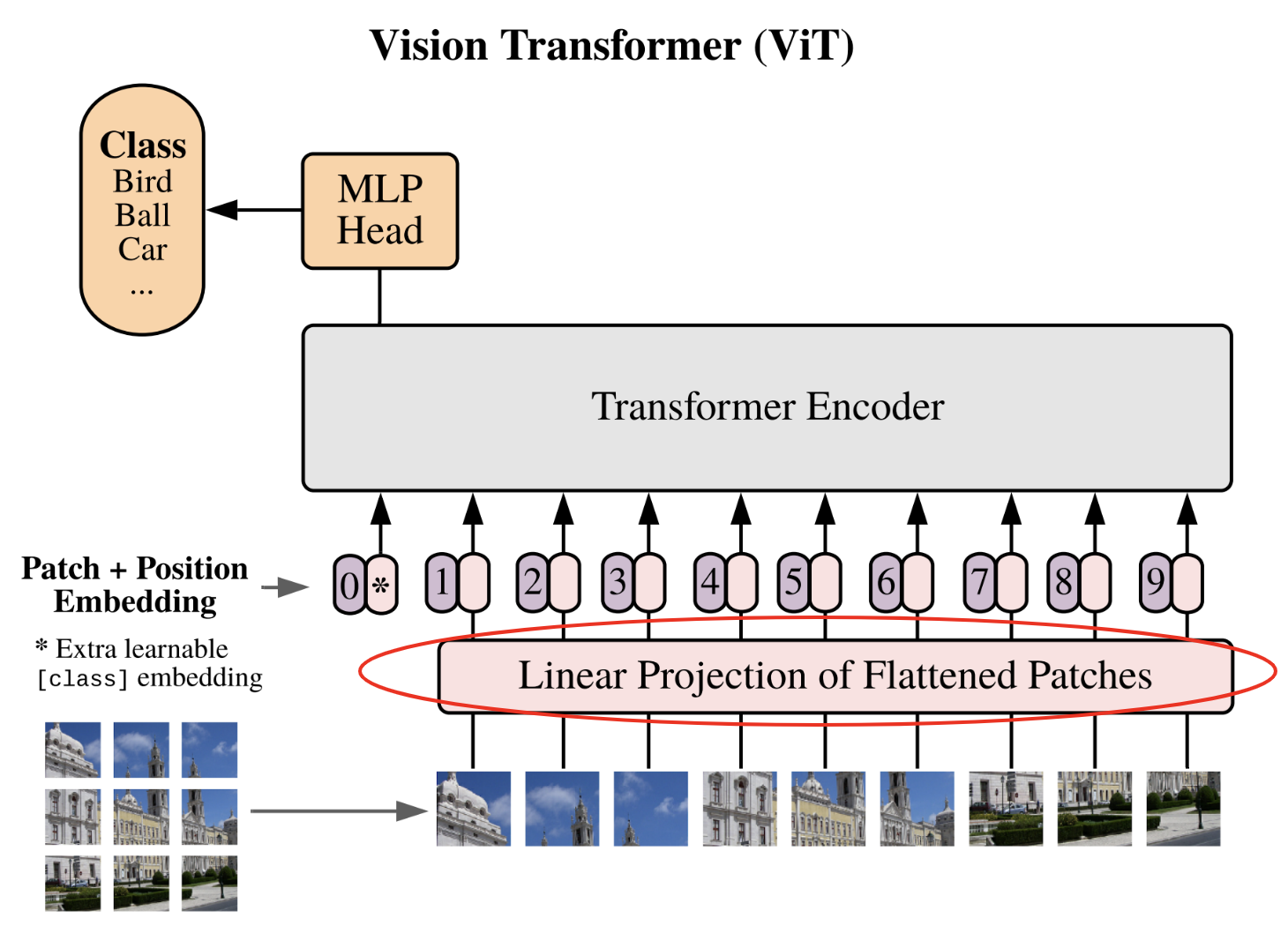
Cette étape est l’équivalent de l’étape de conversion des tokens à l’aide de la table d’embedding. Cette fois-ci, on va convertir nos patchs aplatis en vecteurs de dimension fixe pour que ces vecteurs puissent être traités par le transformer. Définissons notre dimension d’embedding et notre couche de projection :

n_embd = 64
proj_layer = nn.Linear(C*patch_size*patch_size, n_embd)

C’est tout, ce n’est pas l’étape la plus compliquée.

Embedding de position et class token

Passons à la dernière étape avant les couches transformers (qui sont déjà implémentées).

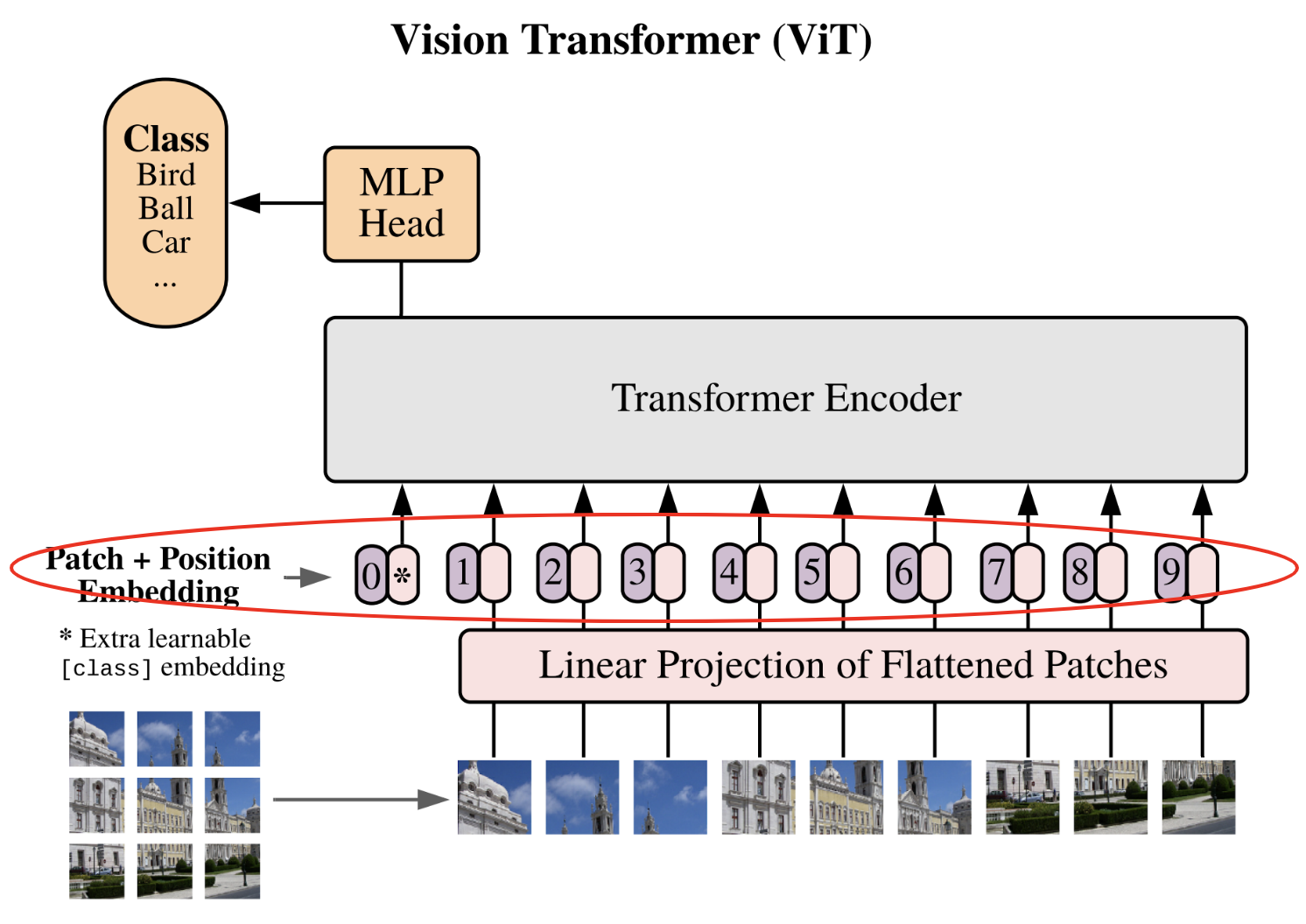
Cette étape contient en fait 2 étapes distinctes :

• L’ajout d’un embedding de position : comme dans le GPT, le transformer n’a pas d’information préalable sur la position du patch dans l’image. Pour cela, on va simplement ajouter un embedding dédié à cela, ce qui permettra au réseau d’avoir une notion de position relative des patchs.

• L’ajout d’un class token : Cette étape est nouvelle car elle n’était pas nécessaire dans le GPT. L’idée vient en fait de BERT et est une technique pour faire de la classification à l’aide d’un transformer sans avoir à spécifier de taille de séquence fixe. Sans class token, pour obtenir notre classification, on aurait besoin soit de coller un réseau fully connected à l’ensemble des sorties du transformer (ce qui imposerait une taille de séquence fixe), soit de coller un réseau fully connected à une sortie du transformer choisie au hasard (une sortie correspond à un patch, mais alors comment choisir ce patch sans biais ?). L’ajout du class token permet de répondre à ce problème en ajoutant un token dédié spécifiquement à la classification.

Note : Pour les CNNs, une manière d’éviter le problème de la dimension fixe de l’entrée est d’utiliser un global average pooling en sortie (couche de pooling avec taille de sortie fixe). Cette technique peut aussi être utilisée pour un vision transformer à la place du class token.

# Pour le positional encoding, +1 pour le cls token
pos_emb = nn.Embedding(nb_patches+1, n_embd)
# On ajoute un token cls
cls_token = torch.zeros(1, 1, n_embd)
# On ajoutera ce token cls au début de chaque séquence

Réseau fully connected de classification

Maintenant, passons à la fin du ViT, c’est-à-dire le réseau MLP de classification. Si vous avez suivi l’intérêt du class token, vous comprenez que ce réseau de classification prend en entrée uniquement ce token pour nous sortir la classe prédite.

Encore une fois, c’est une implémentation assez simple. Dans l’article, ils disent qu’ils utilisent un réseau d’une couche cachée pour l’entraînement et uniquement une couche pour un fine-tuning (voir cours 10 pour des précisions sur le fine-tuning). Par souci de simplicité, on utilise une seule couche linéaire pour projeter le class token de sortie dans la dimension du nombre de classes.

classi_head = nn.Linear(n_embd, 10)

Nous disposons maintenant de tous les éléments pour construire notre ViT et l’entraîner !

Création du modèle ViT

On peut maintenant rassembler les morceaux et créer notre vision transformer.

class ViT(nn.Module):
    def __init__(self, n_embed,patch_size,C,n_head,n_layer,nb_patches,dropout=0.) -> None:
        super().__init__()
        self.proj_layer = nn.Linear(C*patch_size*patch_size, n_embed)
        self.pos_emb = nn.Embedding(nb_patches+1, n_embed)
        # Permet de créer cls_token comme un paramètre du réseau
        self.register_parameter(name='cls_token', param=torch.nn.Parameter(torch.zeros(1, 1, n_embed)))
        self.transformer=nn.Sequential(*[TransformerBlock(n_embed, n_head,dropout) for _ in range(n_layer)])
        self.classi_head = nn.Linear(n_embed, 10)
    
    def forward(self,x):
        B,_,_,_=x.shape
        # On découpe l'image en patch et on les applatit
        x = image_to_patches(x, patch_size)
        # On projette dans la dimension n_embed
        x = self.proj_layer(x)
        # On ajoute le token cls
        cls_tokens = self.cls_token.expand(B, -1, -1)
        x = torch.cat((cls_tokens, x), dim=1)
        # On ajoute le positional encoding
        pos_emb = self.pos_emb(torch.arange(x.shape[1], device=x.device))
        x = x + pos_emb
        # On applique les blocks transformer
        x = self.transformer(x)
        # On récupère le token cls
        cls_tokens = x[:, 0]
        # On applique la dernière couche de classification
        x = self.classi_head(cls_tokens)
        return x        

Entraînement de notre ViT

On va entraîner notre modèle ViT sur le dataset CIFAR-10. À noter que les paramètres qu’on a définis sont adaptés pour des images de petites tailles (n_embed et patch_size). Pour traiter des images plus grandes, il faudra adapter ces paramètres. Le code fonctionne avec des tailles différentes tant que la taille de l’image est divisible par la taille du patch.

Chargement des datasets : train, val et test

Chargons le dataset CIFAR-10 et créons nos dataloaders :

Note : Vous pouvez sélectionner une sous-partie du dataset pour accélérer l’entraînement.

classes = ('plane', 'car', 'bird', 'cat','deer', 'dog', 'frog', 'horse', 'ship', 'truck')
# Transformation des données, normalisation et transformation en tensor pytorch
transform = T.Compose([T.ToTensor(),T.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])

# Téléchargement et chargement du dataset
dataset = datasets.CIFAR10(root='./../data', train=True,download=True, transform=transform)
testdataset = datasets.CIFAR10(root='./../data', train=False,download=True, transform=transform)
print("taille d'une image : ",dataset[0][0].shape)


#Création des dataloaders pour le train, validation et test
train_dataset, val_dataset=torch.utils.data.random_split(dataset, [0.8,0.2])
print("taille du train dataset : ",len(train_dataset))
print("taille du val dataset : ",len(val_dataset))
print("taille du test dataset : ",len(testdataset))
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=16,shuffle=True, num_workers=2)
val_loader= torch.utils.data.DataLoader(val_dataset, batch_size=16,shuffle=True, num_workers=2)
test_loader = torch.utils.data.DataLoader(testdataset, batch_size=16,shuffle=False, num_workers=2)

Files already downloaded and verified
Files already downloaded and verified
taille d'une image :  torch.Size([3, 32, 32])
taille du train dataset :  40000
taille du val dataset :  10000
taille du test dataset :  10000

Hyperparamètres et création du modèle

On va maintenant définir nos hyperparamètres d’entraînement et les spécificités du modèle :

patch_size = 8
nb_patches = (32//patch_size)**2
n_embed = 64
n_head = 4
n_layer = 4
epochs = 10
C=3 # Nombre de canaux
lr = 1e-3
model = ViT(n_embed,patch_size,C,n_head,n_layer,nb_patches).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=lr)

Entraînement du modèle

Il est finalement temps d’entraîner notre modèle !

for epoch in range(epochs):
    model.train()
    loss_train = 0
    for i, (images, labels) in enumerate(train_loader):
        images, labels = images.to(device), labels.to(device)
        optimizer.zero_grad()
        output = model(images)
        loss = F.cross_entropy(output, labels)
        loss_train += loss.item()
        loss.backward()
        optimizer.step()
        
    model.eval()
    correct = 0
    total = 0
    loss_val = 0
    with torch.no_grad():
        for images, labels in val_loader:
            images, labels = images.to(device), labels.to(device)
            outputs = model(images)
            loss_val += F.cross_entropy(outputs, labels).item()
            _, predicted = torch.max(outputs.data, 1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()

    print(f"Epoch {epoch}, loss train {loss_train/len(train_loader)}, loss val {loss_val/len(val_loader)},précision {100 * correct / total}")

Epoch 0, loss train 1.6522698682546615, loss val 1.4414834783554078,précision 47.97
Epoch 1, loss train 1.3831321718215943, loss val 1.3656272639274598,précision 50.69
Epoch 2, loss train 1.271412028503418, loss val 1.2726070711135864,précision 55.17
Epoch 3, loss train 1.1935315937042237, loss val 1.2526390438556672,précision 55.52
Epoch 4, loss train 1.1144725002408027, loss val 1.2377954412460328,précision 55.66
Epoch 5, loss train 1.0520227519154548, loss val 1.2067877051830291,précision 56.82
Epoch 6, loss train 0.9839000009179115, loss val 1.2402711957931518,précision 56.93
Epoch 7, loss train 0.9204218792438507, loss val 1.2170260044574737,précision 58.23
Epoch 8, loss train 0.853291154640913, loss val 1.2737546770095824,précision 57.65
Epoch 9, loss train 0.7962572723925113, loss val 1.2941821083545684,précision 58.26

L’entraînement s’est bien passé, on obtient une précision de 58% sur les données de validation. Regardons maintenant nos résultats sur les données de test :

model.eval()
correct = 0
total = 0
with torch.no_grad():
    for images, labels in test_loader:
        images, labels = images.to(device), labels.to(device)
        outputs = model(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print(f"Précision {100 * correct / total}")

Précision 58.49

La précision est du même ordre sur les données de test !

Note : Ce résultat peut paraître assez médiocre, mais il ne faut pas oublier qu’on utilise un petit transformer entraîné sur peu d’epochs. Vous pouvez essayer d’améliorer ce résultat en jouant sur les hyperparamètres.

Note2 : Les auteurs du papier précisent que le transformer n’a pas de “inductive bias” sur les images contrairement aux CNN, et cela provient de l’architecture. Les couches d’un CNN sont invariantes par translation et capturent le voisinage de chaque pixel, tandis que les transformers utilisent principalement l’information globale. En pratique, on constate que sur des “petits” datasets (jusqu’à 1 million d’images), les CNN performent mieux, mais pour des plus grosses quantités de données, les transformers sont plus performants.