Techniques avancées#
Dans ce cours, on va découvrir des techniques pour améliorer la fiabilité et la facilité d’entraînement des réseaux de neurones. Pour illustrer ces techniques, on utilise le dataset MNIST, qui contient des images de chiffres manuscrits de 1 à 9. L’objectif est de faire en sorte que le réseau prenne une image en entrée et identifie le chiffre qu’elle représente.
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision.transforms as T
from torchvision import datasets
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
Création du dataset#
Pour commencer, on télécharge le dataset MNIST. La bibliothèque torchvision permet de gérer les images avec PyTorch et offre des outils pour charger les datasets courants.
transform=T.ToTensor() # Pour convertir les éléments en tensor torch directement
dataset = datasets.MNIST(root='./../data', train=True, download=True,transform=transform)
test_dataset = datasets.MNIST(root='./../data', train=False,transform=transform)
# On peut visualiser les éléments du dataset
plt.imshow(dataset[0][0].permute(1,2,0).numpy(), cmap='gray')
plt.show()
print("Le chiffre sur l'image est un "+str(dataset[0][1]))

Le chiffre sur l'image est un 5
Séparation train/validation/test#
Comme tu as pu le voir, lors du chargement du dataset, on a un train_dataset et un test_dataset. C’est une pratique essentielle pour entraîner un réseau de neurones. En effet, un réseau entraîné sur des données performe bien sur ces mêmes données. Il faut donc créer un dataset de test pour évaluer le modèle sur des données non vues pendant l’entraînement.
En pratique, on utilise 3 sous-datasets :
Le training split pour l’entraînement du modèle.
Le validation split pour évaluer le modèle pendant l’entraînement.
Le test split pour évaluer le modèle à la fin de l’entraînement (c’est le résultat le plus important).
Une pratique courante est d’utiliser un split 60-20-20, c’est-à-dire 60% des données pour l’entraînement, 20% pour la validation et 20% pour le test. Cependant, cette recommandation ne convient pas à tous les datasets. Si le dataset contient beaucoup d’images, on peut réduire la part des données de validation et de test. Par exemple, pour des datasets de plusieurs milliards d’images, on utilise souvent des splits 98-1-1 ou même 99.8-0.1-0.1.
#Le train et test sont déjà séparé, on va donc séparer le train_dataset en train et validation
train_dataset, validation_dataset=torch.utils.data.random_split(dataset, [0.8,0.2])
# Création des dataloaders pour séparer en mini-batch automatiquement
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
val_loader= DataLoader(validation_dataset, batch_size=64, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False)
Création et entraînement d’un premier modèle#
Comme dans le notebook précédent, on crée un modèle entièrement connecté pour l’entraînement. Comme les données d’entrée sont des images de taille \(28 \times 28\), il faut les convertir en vecteur 1D de taille \(28 \times 28=784\) pour les faire passer dans le réseau.
class mlp(nn.Module):
def __init__(self, *args, **kwargs) -> None:
super().__init__(*args, **kwargs)
self.fc1=nn.Linear(784,256) # première couche cachée
self.fc2=nn.Linear(256,256) # seconde couche cachée
self.fc3=nn.Linear(256,10) # couche de sortie
# La fonction forward est la fonction appelée lorsqu'on fait model(x)
def forward(self,x):
x=x.view(-1,28*28) # Pour convertir l'image de taille 28x28 en tensor de taille 784
x=F.relu(self.fc1(x)) # le F.relu permet d'appliquer la fonction d'activation ReLU sur la sortie de notre couche
x=F.relu(self.fc2(x))
output=self.fc3(x)
return output
model = mlp()
print(model)
print("Nombre de paramètres", sum(p.numel() for p in model.parameters()))
mlp(
(fc1): Linear(in_features=784, out_features=256, bias=True)
(fc2): Linear(in_features=256, out_features=256, bias=True)
(fc3): Linear(in_features=256, out_features=10, bias=True)
)
Nombre de paramètres 269322
Fonction de perte#
Pour la fonction de perte, on utilise la cross entropy loss de PyTorch, qui correspond à la fonction de perte de la régression logistique pour un nombre de classes supérieur à 2. La fonction de perte s’écrit comme suit : \(\text{Cross Entropy Loss} = -\frac{1}{N} \sum_{i=1}^{N} \sum_{c=1}^{C} y_{ic} \log(p_{ic})\) où :
\(N\) est le nombre d’exemples dans le mini-batch.
\(C\) est le nombre de classes.
\(y_{ic}\) est la valeur cible (\(1\) si l’exemple appartient à la classe \(c\) et \(0\) sinon).
\(p_{ic}\) est la prédiction de la probabilité d’appartenance à la classe \(c\).
# En pytorch
criterion = nn.CrossEntropyLoss()
Hyperparamètres et entraînement#
epochs=5
learning_rate=0.001
optimizer=torch.optim.Adam(model.parameters(),lr=learning_rate)
Entraînement du modèle (peut durer quelques minutes selon la puissance de ton ordinateur).
for i in range(epochs):
loss_train=0
for images, labels in train_loader:
preds=model(images)
loss=criterion(preds,labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
loss_train+=loss
if i % 1 == 0:
print(f"step {i} train loss {loss_train/len(train_loader)}")
loss_val=0
for images, labels in val_loader:
with torch.no_grad(): # permet de ne pas calculer les gradients
preds=model(images)
loss=criterion(preds,labels)
loss_val+=loss
if i % 1 == 0:
print(f"step {i} val loss {loss_val/len(val_loader)}")
step 0 train loss 0.29076647758483887
step 0 val loss 0.15385286509990692
step 1 train loss 0.10695428401231766
step 1 val loss 0.10097559541463852
step 2 train loss 0.07086848467588425
step 2 val loss 0.09286081790924072
step 3 train loss 0.05028771981596947
step 3 val loss 0.08867377787828445
step 4 train loss 0.04254501312971115
step 4 val loss 0.0835222601890564
Vérification du modèle sur les données de test#
Maintenant que le modèle est entraîné, on peut vérifier ses performances sur le testing split.
correct = 0
total = 0
for images,labels in test_loader:
with torch.no_grad():
preds=model(images)
_, predicted = torch.max(preds.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
test_acc = 100 * correct / total
print("Précision du modèle en phase de test : ",test_acc)
Précision du modèle en phase de test : 97.69
Notre modèle obtient une très bonne précision en phase de test, ce qui est un bon signe. Cependant, on remarque que, lors de l’entraînement, le loss de training est plus bas que le loss de validation. C’est un point important à considérer, car cela signifie que le modèle est en léger overfitting.
Overfitting et underfitting#
Un élément clé de l’apprentissage profond est la capacité du modèle à ne pas overfitter les données d’entraînement. L’overfitting correspond à un modèle qui a trop bien appris sur les données d’entraînement, mais qui n’est pas capable de généraliser à de nouveaux éléments issus de la même distribution. Pour comprendre le principe, voici une figure qui montre la différence entre l’underfitting (modèle trop simple incapable d’apprendre la complexité des données), un modèle bien entraîné et l’overfitting.
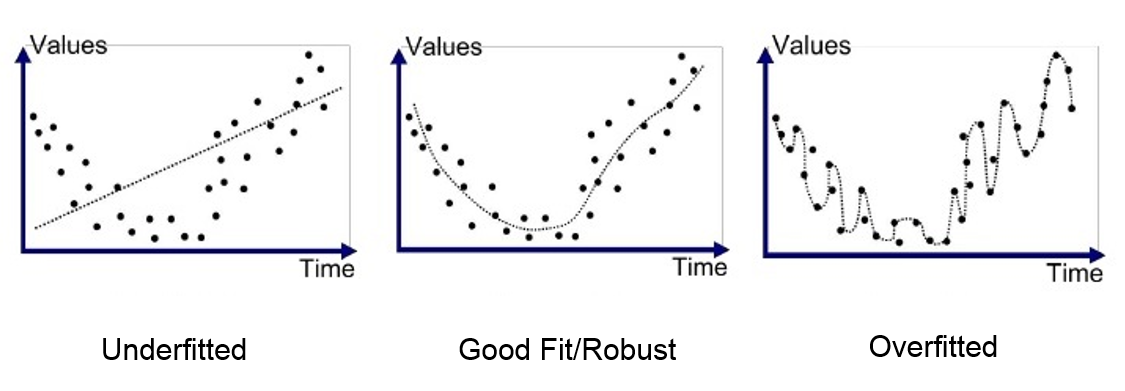
Dans le cas le plus critique de l’overfitting, le modèle a une précision presque parfaite sur les données d’entraînement, mais est mauvais sur les données de validation et de test. Dans ce cours, on va introduire 2 méthodes pour éviter ce problème d’overfitting.
Régularisation L2#
La régularisation L2 est une méthode qui consiste à ajouter une pénalité à la perte basée sur la valeur des poids du modèle. Cette pénalité est proportionnelle au carré des valeurs des poids du modèle (à noter qu’il existe aussi la régularisation L1, qui est linéairement proportionnelle aux valeurs des poids du modèle). Cette pénalité encourage les poids du modèle à rester petits et moins sensibles au bruit des données d’entraînement. On peut formuler la régularisation L2 de cette manière : \(L(w) = L_0(w) + \lambda \sum_{i=1}^{n} w_i^2\) où :
\(L(w)\) est la perte régularisée.
\(L_0(w)\) est la fonction de perte classique.
\(\lambda\) est le coefficient de régularisation.
\(w_i\) est un poids du modèle.
Pour en apprendre plus sur la régularisation L2, tu peux consulter le cours bonus sur la régularisation ou ce blogpost.
Refaisons l’entraînement en ajoutant la régularisation. En PyTorch, la régularisation s’utilise en ajoutant le paramètre weight_decay à notre optimizer. La valeur de weight_decay correspond au \(\lambda\) de l’équation précédente.
model_with_reg=mlp()
epochs=5
learning_rate=0.001
optimizer=torch.optim.Adam(model_with_reg.parameters(),lr=learning_rate,weight_decay=1e-5)
for i in range(epochs):
loss_train=0
for images, labels in train_loader:
preds=model_with_reg(images)
loss=criterion(preds,labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
loss_train+=loss
if i % 1 == 0:
print(f"step {i} train loss {loss_train/len(train_loader)}")
loss_val=0
for images, labels in val_loader:
with torch.no_grad(): # permet de ne pas calculer les gradients
preds=model_with_reg(images)
loss=criterion(preds,labels)
loss_val+=loss
if i % 1 == 0:
print(f"step {i} val loss {loss_val/len(val_loader)}")
step 0 train loss 0.2986273467540741
step 0 val loss 0.1439662128686905
step 1 train loss 0.11165566742420197
step 1 val loss 0.10781095176935196
step 2 train loss 0.07492929697036743
step 2 val loss 0.09555892646312714
step 3 train loss 0.05378309637308121
step 3 val loss 0.08672302216291428
step 4 train loss 0.041800014674663544
step 4 val loss 0.0883878618478775
correct = 0
total = 0
for images,labels in test_loader:
with torch.no_grad():
preds=model_with_reg(images)
_, predicted = torch.max(preds.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
test_acc = 100 * correct / total
print("Précision du modèle en phase de test : ",test_acc)
Précision du modèle en phase de test : 97.73
La différence n’est pas flagrante, mais on constate une diminution de la différence entre la perte de validation et la perte d’entraînement.
Intuition : La régularisation L2 fonctionne parce qu’en pénalisant les grands coefficients, elle favorise des solutions où les poids sont répartis de manière plus uniforme. Cela réduit la sensibilité du modèle aux variations spécifiques des données d’entraînement et améliore ainsi la robustesse et la généralisation du modèle.
Dropout#
Une autre méthode de régularisation est le dropout. Cette méthode consiste à désactiver aléatoirement un pourcentage de neurones dans le réseau à chaque étape de l’entraînement (les poids désactivés changent pendant l’entraînement). Chaque neurone d’une couche a une probabilité \(p\) d’être désactivé.
Cette technique force le réseau à ne pas se reposer sur certains neurones, mais plutôt à apprendre des représentations plus robustes et qui généralisent mieux. On peut voir le dropout comme une sorte d’ensemble de modèles où chaque modèle est différent (car certains neurones sont désactivés). Lors de la phase de test, on prend la “moyenne” de ces différents modèles. Lors de la phase de test, le dropout est désactivé.
Pour appliquer le dropout, il faut l’ajouter directement dans l’architecture du réseau.
class mlp_dropout(nn.Module):
def __init__(self, *args, **kwargs) -> None:
super().__init__(*args, **kwargs)
self.fc1=nn.Linear(784,256)
self.dropout1 = nn.Dropout(0.2) # on désactive 20% des neurones aléatoirement
self.fc2=nn.Linear(256,256)
self.dropout2 = nn.Dropout(0.2) # on désactive 20% des neurones aléatoirement
self.fc3=nn.Linear(256,10)
def forward(self,x):
x=x.view(-1,28*28)
x=F.relu(self.dropout1(self.fc1(x)))
x=F.relu(self.dropout2(self.fc2(x)))
output=self.fc3(x)
return output
model_with_dropout=mlp_dropout()
epochs=5
learning_rate=0.001
optimizer=torch.optim.Adam(model_with_dropout.parameters(),lr=learning_rate)
for i in range(epochs):
loss_train=0
for images, labels in train_loader:
preds=model_with_dropout(images)
loss=criterion(preds,labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
loss_train+=loss
if i % 1 == 0:
print(f"step {i} train loss {loss_train/len(train_loader)}")
loss_val=0
for images, labels in val_loader:
with torch.no_grad(): # permet de ne pas calculer les gradients
preds=model_with_dropout(images)
loss=criterion(preds,labels)
loss_val+=loss
if i % 1 == 0:
print(f"step {i} val loss {loss_val/len(val_loader)}")
step 0 train loss 0.3267715573310852
step 0 val loss 0.19353896379470825
step 1 train loss 0.13504144549369812
step 1 val loss 0.14174170792102814
step 2 train loss 0.10012412816286087
step 2 val loss 0.13484247028827667
step 3 train loss 0.07837768644094467
step 3 val loss 0.10895466059446335
step 4 train loss 0.0631122887134552
step 4 val loss 0.10599609464406967
correct = 0
total = 0
for images,labels in test_loader:
with torch.no_grad():
preds=model_with_dropout(images)
_, predicted = torch.max(preds.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
test_acc = 100 * correct / total
print("Précision du modèle en phase de test : ",test_acc)
Précision du modèle en phase de test : 96.96
On constate à nouveau une légère amélioration du résultat de l’entraînement.
Intuition : Le dropout améliore la généralisation en désactivant aléatoirement des neurones pendant l’entraînement. Cela empêche le modèle de trop se fier à certains neurones et force une distribution plus robuste et diversifiée des caractéristiques apprises.
Batch Normalization#
Une autre technique pour améliorer l’entraînement d’un réseau de neurones est la Batch Normalization (BatchNorm). Le principe est de normaliser les entrées de chaque couche du réseau avec une distribution ayant une moyenne nulle et une variance de 1. La normalisation s’effectue sur le batch complet de la manière suivante :
Pour un mini-batch \(B\) avec activations \(x\) :
\(\mu_B = \frac{1}{m} \sum_{i=1}^m x_i\) : la moyenne des activations \(x_i\) des \(m\) éléments.
\(\sigma_B^2 = \frac{1}{m} \sum_{i=1}^m (x_i - \mu_B)^2\) : la variance des activations \(x_i\) des \(m\) éléments.
\(\hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}\) : la valeur de \(x_i\) normalisée.
\(y_i = \gamma \hat{x}_i + \beta\) : l’ajout des paramètres \(\gamma\) et \(\beta\) permet au réseau d’apprendre les distributions d’activation optimales.
où :
\(m\) est la taille du mini-batch \(B\).
\(\epsilon\) est une petite constante ajoutée pour éviter la division par zéro.
\(\gamma\) et \(\beta\) sont des paramètres apprenables.
En pratique, on constate 4 principaux avantages lors de l’utilisation de la BatchNorm :
Accélération de l’entraînement : La normalisation des entrées de chaque couche permet d’utiliser un learning rate plus élevé et donc d’accélérer la convergence de l’entraînement.
Réduction de la sensibilité à l’initialisation des poids : La BatchNorm permet de stabiliser la distribution des activations, ce qui rend le réseau moins sensible à l’initialisation des poids.
Amélioration de la généralisation : Comme le dropout et la régularisation L2, la BatchNorm agit comme une forme de régularisation. Cela est dû au bruit induit par le fait de normaliser sur le batch.
Réduction du “Internal Covariate Shift” : La stabilisation des activations tout au long du réseau permet de réduire le changement des distributions des couches internes, ce qui facilite l’apprentissage.
Ce qu’il faut retenir, c’est que la BatchNorm offre de nombreux avantages et il est donc conseillé de l’utiliser systématiquement.
Il existe également d’autres techniques de normalisation comme la LayerNorm, la InstanceNorm, la GroupNorm et d’autres … Pour en apprendre plus sur la batch normalization, tu peux faire le cours bonus sur la batch norm, lire le papier ou le blogpost. Pour avoir des informations supplémentaires sur l’intérêt de la normalisation pour l’entraînement des réseaux de neurones, tu peux consulter le blogpost.
Pour implémenter la BatchNorm en PyTorch, il faut l’ajouter directement dans la construction du modèle. À noter qu’on applique souvent la BatchNorm avant la fonction d’activation, mais les deux approches sont possibles (avant ou après).
class mlp_bn(nn.Module):
def __init__(self, *args, **kwargs) -> None:
super().__init__(*args, **kwargs)
self.fc1=nn.Linear(784,256)
self.bn1=nn.BatchNorm1d(256) # Batch Normalization
self.fc2=nn.Linear(256,256)
self.bn2=nn.BatchNorm1d(256) # Batch Normalization
self.fc3=nn.Linear(256,10)
def forward(self,x):
x=x.view(-1,28*28)
x=F.relu(self.bn1(self.fc1(x)))
x=F.relu(self.bn1(self.fc2(x)))
output=self.fc3(x)
return output
model_with_bn=mlp_bn()
epochs=5
learning_rate=0.001
optimizer=torch.optim.Adam(model_with_bn.parameters(),lr=learning_rate)
for i in range(epochs):
loss_train=0
for images, labels in train_loader:
preds=model_with_bn(images)
loss=criterion(preds,labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
loss_train+=loss
if i % 1 == 0:
print(f"step {i} train loss {loss_train/len(train_loader)}")
loss_val=0
for images, labels in val_loader:
with torch.no_grad(): # permet de ne pas calculer les gradients
preds=model_with_bn(images)
loss=criterion(preds,labels)
loss_val+=loss
if i % 1 == 0:
print(f"step {i} val loss {loss_val/len(val_loader)}")
step 0 train loss 0.20796926319599152
step 0 val loss 0.1327729970216751
step 1 train loss 0.09048832952976227
step 1 val loss 0.10177803039550781
step 2 train loss 0.0635765939950943
step 2 val loss 0.09861738979816437
step 3 train loss 0.045849185436964035
step 3 val loss 0.09643400460481644
step 4 train loss 0.0397462323307991
step 4 val loss 0.08524414896965027
correct = 0
total = 0
for images,labels in test_loader:
with torch.no_grad():
preds=model_with_bn(images)
_, predicted = torch.max(preds.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
test_acc = 100 * correct / total
print("Précision du modèle en phase de test : ",test_acc)
Précision du modèle en phase de test : 97.19
Comme tu peux le voir, la BatchNorm permet d’obtenir un meilleur score sur nos données dans les mêmes conditions d’entraînement.