Construisons un GPT à partir de zéro#
Ce notebook explique comment créer un modèle de langage pour prédire le prochain caractère, en s’appuyant sur l’architecture du transformer (plus précisément le décodeur).
Pour cela, on utilise un fichier texte moliere.txt contenant tous les dialogues des pièces de Molière.
Ce dataset a été créé à partir des œuvres complètes de Molière disponibles sur Gutenberg.org. J’ai nettoyé les données pour ne conserver que les dialogues.
import torch
import torch.nn as nn
from torch.nn import functional as F
# Pour utiliser le GPU automatiquement si vous en avez un
device = 'cuda' if torch.cuda.is_available() else 'cpu'
Lecture du dataset#
Commençons par ouvrir et visualiser le contenu de notre dataset.
with open('moliere.txt', 'r', encoding='utf-8') as f:
text = f.read()
print("Nombre de caractères dans le dataset : ", len(text))
Nombre de caractères dans le dataset : 1687290
Affichons les 250 premiers caractères :
print(text[:250])
VALÈRE.
Eh bien, Sabine, quel conseil me donnes-tu?
SABINE.
Vraiment, il y a bien des nouvelles. Mon oncle veut résolûment que ma
cousine épouse Villebrequin, et les affaires sont tellement avancées,
que je crois qu'ils eussent été mariés dès aujo
Utilisons set() pour récupérer les caractères uniques présents dans le dataset.
chars = sorted(list(set(text)))
vocab_size = len(chars)
print(''.join(chars))
print("Nombre de caractères différents : ", vocab_size)
!'(),-.:;?ABCDEFGHIJKLMNOPQRSTUVXYZabcdefghijlmnopqrstuvxyz«»ÇÈÉÊÏàâæçèéêëìîïòôùûŒœ
Nombre de caractères différents : 85
Création du dataset d’entraînement#
Comme dans le cours 5, on va créer un mapping pour convertir des caractères en entiers. Ce mapping est une forme très simple de tokenization.
Point rapide sur la tokenization#
Qu’est-ce que la tokenization ? La tokenization est le processus qui convertit un texte en séquence d’entiers. Chaque entier peut représenter un caractère, un groupe de caractères ou un mot, selon la méthode utilisée.
Équilibre entre vocabulaire et taille de séquence Un bon tokenizer trouve un équilibre entre la taille du vocabulaire (26 pour l’alphabet et environ 100 000 pour les mots en français). Un vocabulaire trop petit augmente la longueur des séquences (ex. : “Bonjour” devient 7 tokens si on utilise des caractères, ou 1 token si on utilise des mots). En pratique, les extrêmes sont problématiques, et on cherche un juste milieu.
Tokenizers populaires Les tokenizers sont essentiels pour le bon fonctionnement d’un modèle de langage. Leur conception dépend de la méthode et des données d’entraînement. Parmi les plus utilisés, on trouve SentencePiece de Google et tiktoken d’OpenAI.
# Creation d'un mapping de caractère à entiers et inversement
stoi = { ch:i for i,ch in enumerate(chars) }
itos = { i:ch for i,ch in enumerate(chars) }
encode = lambda s: [stoi[c] for c in s] # encore : prend un string et output une liste d'entiers
decode = lambda l: ''.join([itos[i] for i in l]) # decode: prend une liste d'entiers et output un string
print(encode("Bonjour à tous"))
print(decode(encode("Bonjour à Tous")))
[13, 50, 49, 46, 50, 56, 53, 1, 68, 1, 55, 50, 56, 54]
Bonjour à Tous
On va transformer notre dataset en séquences d’entiers et le stocker sous forme de tenseurs PyTorch.
data = torch.tensor(encode(text), dtype=torch.long)
print(data[:250]) # Les 250 premiers caractères encodé
tensor([33, 12, 23, 64, 29, 16, 8, 0, 0, 16, 44, 1, 38, 45, 41, 49, 6, 1,
30, 37, 38, 45, 49, 41, 6, 1, 52, 56, 41, 47, 1, 39, 50, 49, 54, 41,
45, 47, 1, 48, 41, 1, 40, 50, 49, 49, 41, 54, 7, 55, 56, 11, 0, 0,
30, 12, 13, 20, 25, 16, 8, 0, 0, 33, 53, 37, 45, 48, 41, 49, 55, 6,
1, 45, 47, 1, 59, 1, 37, 1, 38, 45, 41, 49, 1, 40, 41, 54, 1, 49,
50, 56, 57, 41, 47, 47, 41, 54, 8, 1, 24, 50, 49, 1, 50, 49, 39, 47,
41, 1, 57, 41, 56, 55, 1, 53, 73, 54, 50, 47, 82, 48, 41, 49, 55, 1,
52, 56, 41, 1, 48, 37, 0, 39, 50, 56, 54, 45, 49, 41, 1, 73, 51, 50,
56, 54, 41, 1, 33, 45, 47, 47, 41, 38, 53, 41, 52, 56, 45, 49, 6, 1,
41, 55, 1, 47, 41, 54, 1, 37, 42, 42, 37, 45, 53, 41, 54, 1, 54, 50,
49, 55, 1, 55, 41, 47, 47, 41, 48, 41, 49, 55, 1, 37, 57, 37, 49, 39,
73, 41, 54, 6, 0, 52, 56, 41, 1, 46, 41, 1, 39, 53, 50, 45, 54, 1,
52, 56, 3, 45, 47, 54, 1, 41, 56, 54, 54, 41, 49, 55, 1, 73, 55, 73,
1, 48, 37, 53, 45, 73, 54, 1, 40, 72, 54, 1, 37, 56, 46, 50])
On va maintenant découper notre texte en parties d’entraînement et de validation. On prend un ratio de 0.9-0.1.
n = int(0.9*len(data)) # 90% pour le train et 10% pour la validation
train_data = data[:n]
val_data = data[n:]
Pour notre modèle de langage, on va aussi définir une taille de contexte block_size.
block_size = 8
train_data[:block_size+1]
tensor([33, 12, 23, 64, 29, 16, 8, 0, 0])
Ici, les 8 premiers caractères représentent le contexte et le 9ème est le label. Ce simple exemple regroupe en fait plusieurs cas, car notre modèle doit prédire le prochain caractère quel que soit le contexte. Dans cette liste, on a donc 8 exemples :
x = train_data[:block_size]
y = train_data[1:block_size+1]
for t in range(block_size):
context = x[:t+1]
target = y[t]
print(f"Quand l'entrée est {context.numpy()} le label est : {target}")
Quand l'entrée est [33] le label est : 12
Quand l'entrée est [33 12] le label est : 23
Quand l'entrée est [33 12 23] le label est : 64
Quand l'entrée est [33 12 23 64] le label est : 29
Quand l'entrée est [33 12 23 64 29] le label est : 16
Quand l'entrée est [33 12 23 64 29 16] le label est : 8
Quand l'entrée est [33 12 23 64 29 16 8] le label est : 0
Quand l'entrée est [33 12 23 64 29 16 8 0] le label est : 0
On sait maintenant comment créer un ensemble d’entrées/étiquettes à partir d’un seul exemple. Adaptons cette méthode pour un traitement par batch :
batch_size = 4 # La taille de batch (les séquences calculés en parallèles)
block_size = 8 # La taille de contexte maximale pour une prédiction du modèle
def get_batch(split):
# On genere un batch de données (sur train ou val)
data = train_data if split == 'train' else val_data
#On génére batch_size indice de début de séquence pris au hasard dans le dataset
ix = torch.randint(len(data) - block_size, (batch_size,))
# On stocke dans notre tenseur torch
x = torch.stack([data[i:i+block_size] for i in ix])
y = torch.stack([data[i+1:i+block_size+1] for i in ix])
x, y = x.to(device), y.to(device) # On met les sur le GPU si on en a un
return x, y
xb, yb = get_batch('train')
print('Entrée : ')
print(xb.shape)
print(xb)
print('Labels :')
print(yb.shape)
print(yb)
Entrée :
torch.Size([4, 8])
tensor([[53, 69, 39, 41, 2, 0, 0, 27],
[53, 1, 56, 49, 1, 39, 84, 56],
[54, 11, 0, 0, 24, 12, 30, 14],
[ 1, 51, 72, 53, 41, 8, 0, 0]], device='cuda:0')
Labels :
torch.Size([4, 8])
tensor([[69, 39, 41, 2, 0, 0, 27, 19],
[ 1, 56, 49, 1, 39, 84, 56, 53],
[11, 0, 0, 24, 12, 30, 14, 12],
[51, 72, 53, 41, 8, 0, 0, 33]], device='cuda:0')
Chacun de ces 4 exemples regroupe 8 exemples distincts (comme expliqué précédemment), ce qui fait un total de 32 exemples.
Modèle bigramme#
Dans le cours 5 sur le NLP, on a vu le bigramme, le modèle de langage le plus simple. Il prédit le prochain caractère à partir d’un seul caractère de contexte. Notons \(B\) pour la taille du batch, \(T\) pour la taille du block et \(C\) pour la taille du vocabulaire.
Pour tester ses performances sur le dataset moliere.txt, implémentons-le rapidement en PyTorch :
class BigramLanguageModel(nn.Module):
def __init__(self, vocab_size):
super().__init__()
# Chaque token va directement lire la valeur du prochain à partir d'une look-up table entrainé
self.token_embedding_table = nn.Embedding(vocab_size, vocab_size)
def forward(self, idx, targets=None):
# Taille (B,T)
logits = self.token_embedding_table(idx)
# Taille (B,T,C)
# Pour gérer le cas de la génération (pas de target)
if targets is None:
loss = None
else: # Cas de l'entraînement
B, T, C = logits.shape
logits = logits.view(B*T, C)
targets = targets.view(B*T)
loss = F.cross_entropy(logits, targets)
return logits, loss
def generate(self, idx, max_new_tokens):
# idx est de la taille (B,T) avec T le contexte actuel
for _ in range(max_new_tokens):
# Forward du modèle pour récuperer les prédictions
logits, _ = self(idx)
# On prend uniquement le dernier caractère
logits = logits[:, -1, :] # devient (B, C)
# On applique la softmax pour récuperer les probabilités
probs = F.softmax(logits, dim=-1) # (B, C)
# On sample avec torch.multinomial
idx_next = torch.multinomial(probs, num_samples=1) # devient (B, 1)
# On ajouter l'élément sample à la séquence actuelle
idx = torch.cat((idx, idx_next), dim=1) # (B, T+1)
return idx
m = BigramLanguageModel(vocab_size).to(device)
logits, loss = m(xb, yb)
print(logits.shape)
print(loss)
torch.Size([32, 85])
tensor(4.6802, device='cuda:0', grad_fn=<NllLossBackward0>)
Le modèle est implémenté mais non entraîné. Si on le teste comme ça, on obtient des résultats catastrophiques :
base=torch.zeros((1, 1), dtype=torch.long).to(device) # Le premier élément est un 0 (token de retour à la ligne)
# On génère 100 éléments
print(decode(m.generate(idx = base , max_new_tokens=100)[0].tolist()))
CZjb!DzPGŒR?'hô.ù
cddhhf,séÇqmp.ÉMjôCùÊF:TAFYèL àP;zbVmëtuPipL.ôHtSEé,t:æéÉYÈìïë?VGYxoùyçnï'lpôHà!ô
C’est tout simplement aléatoire, ce qui est logique car le modèle est initialisé aléatoirement.
On va maintenant entraîner le modèle :
optimizer = torch.optim.AdamW(m.parameters(), lr=1e-3)
batch_size = 32
steps=10000
for step in range(steps): # Nombre d'étape d'entraînement (élements traités = steps*batch_size)
# On récupère un batch de données aléatoires
xb, yb = get_batch('train')
# On calcule le loss
logits, loss = m(xb, yb)
optimizer.zero_grad(set_to_none=True)
# Retropropagation
loss.backward()
# Mise à jour des poids du modèle
optimizer.step()
print(loss.item())
/home/aquilae/anaconda3/envs/dev/lib/python3.11/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
from .autonotebook import tqdm as notebook_tqdm
2.2493152618408203
Générons à partir de notre modèle entraîné :
print(decode(m.generate(idx = torch.zeros((1, 1), dtype=torch.long).to(device), max_new_tokens=300)[0].tolist()))
ELASGOXûÏï!
ANDann donde se ns ntrar pous fa àTEn!.
TELITEL'enomouvûûKbeue
SGAvore oue mesontre
t de pou n qur quvabou qude dente je père e em'eni
La d'euhèmpon, j'es en paiqus de rau plenoilà jonont DARLysontausqus es ei voisangur s ve.
DO lar dire tré quseuqu'arme à ai? t pe ne ndome l pa,
On constate une amélioration dans la structuration des données, et certains mots semblent presque corrects. Mais le résultat reste catastrophique, ce qui est logique car le bigramme est un modèle trop simple.
Self-Attention#
On va maintenant présenter pas à pas le concept de self-attention, un élément clé de l’architecture des transformers.
Qu’est-ce qu’on veut faire ?#
Commençons par une idée simple. On a un tenseur de taille \((B,T,C)\). On veut que chaque élément \(T\) soit la moyenne de l’élément actuel et des éléments précédents, sans tenir compte des éléments suivants. C’est la façon la plus simple de donner de l’importance aux éléments précédents pour prédire la valeur actuelle (c’est l’idée derrière le mécanisme d’attention).
En Python, on peut implémenter cette idée de cette manière :
# Création de notre tenseur random
B,T,C = 4,4,2
x = torch.randn(B,T,C)
x.shape
torch.Size([4, 4, 2])
# Calcul de la moyenne des éléments précédents (incluant l'élément actuel) pour chaque valeur.
xbow = torch.zeros((B,T,C))
for b in range(B):
for t in range(T):
xprev = x[b,:t+1] # (t,C)
xbow[b,t] = torch.mean(xprev, 0)
print(x[0])
print(xbow[0])
tensor([[ 1.5023, -0.5911],
[ 1.0199, -0.2976],
[-1.7581, 0.0969],
[ 0.7444, -0.3360]])
tensor([[ 1.5023, -0.5911],
[ 1.2611, -0.4443],
[ 0.2547, -0.2639],
[ 0.3771, -0.2819]])
On obtient bien ce qu’on voulait : chaque élément correspond à la moyenne de l’élément actuel avec les éléments précédents.
Cependant, on sait que les boucles for sont inefficaces pour les calculs. On préférerait une opération matricielle pour effectuer la même chose.
Rappel sur la multiplication de matrices#
Multiplication matricielle : Matrice \((3 \times 3)\) par Matrice \((3 \times 2)\) Matrices de départ
Soit la matrice \(A\) de dimensions \((3 \times 3)\) :
\(A = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}\)
et la matrice \(B\) de dimensions \((3 \times 2)\) :
\(B = \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \\ b_{31} & b_{32} \end{pmatrix}\)
La multiplication matricielle \(C = A \times B\) donne une matrice \(C\) de dimensions \((3 \times 2)\) :
\(C = \begin{pmatrix} c_{11} & c_{12} \\ c_{21} & c_{22} \\ c_{31} & c_{32} \end{pmatrix}\)
où chaque élément \(c_{ij}\) est calculé comme suit :
\(c_{ij} = \sum_{k=1}^{3} a_{ik} \cdot b_{kj}\)
C’est-à-dire :
\(c_{11} = a_{11}b_{11} + a_{12}b_{21} + a_{13}b_{31}\)
\(c_{12} = a_{11}b_{12} + a_{12}b_{22} + a_{13}b_{32}\)
\(c_{21} = a_{21}b_{11} + a_{22}b_{21} + a_{23}b_{31}\)
\(c_{22} = a_{21}b_{12} + a_{22}b_{22} + a_{23}b_{32}\)
\(c_{31} = a_{31}b_{11} + a_{32}b_{21} + a_{33}b_{31}\)
\(c_{32} = a_{31}b_{12} + a_{32}b_{22} + a_{33}b_{32}\)
Voici un exemple en Python qui illustre cela :
a = torch.ones(3, 3)
b = torch.randint(0,10,(3,2)).float()
c = a @ b
print('a=')
print(a)
print('--')
print('b=')
print(b)
print('--')
print('c=')
print(c)
a=
tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
--
b=
tensor([[7., 6.],
[5., 0.],
[1., 8.]])
--
c=
tensor([[13., 14.],
[13., 14.],
[13., 14.]])
L’astuce mathématique pour le self-attention#
C’est maintenant que la magie opère. Lorsque, au lieu d’une matrice de 1, on prend une matrice triangulaire inférieure et qu’on refait le calcul :
a = torch.tril(torch.ones(3, 3))
b = torch.randint(0,10,(3,2)).float()
c = a @ b
print('a=')
print(a)
print('--')
print('b=')
print(b)
print('--')
print('c=')
print(c)
a=
tensor([[1., 0., 0.],
[1., 1., 0.],
[1., 1., 1.]])
--
b=
tensor([[1., 2.],
[1., 4.],
[6., 6.]])
--
c=
tensor([[ 1., 2.],
[ 2., 6.],
[ 8., 12.]])
Chaque valeur de la matrice est la somme de la valeur actuelle et des valeurs précédentes. C’est presque ce qu’on veut ! Il suffit alors de normaliser selon les lignes :
a = torch.tril(torch.ones(3, 3))
a = a / torch.sum(a, 1, keepdim=True)
b = torch.randint(0,10,(3,2)).float()
c = a @ b
print('a=')
print(a)
print('--')
print('b=')
print(b)
print('--')
print('c=')
print(c)
a=
tensor([[1.0000, 0.0000, 0.0000],
[0.5000, 0.5000, 0.0000],
[0.3333, 0.3333, 0.3333]])
--
b=
tensor([[1., 2.],
[8., 6.],
[9., 8.]])
--
c=
tensor([[1.0000, 2.0000],
[4.5000, 4.0000],
[6.0000, 5.3333]])
Et voilà, le tour est joué ! On a remplacé notre double boucle for par une simple multiplication matricielle et une normalisation des valeurs.
On va maintenant l’utiliser pour calculer xbow et comparer sa valeur avec celle calculée avec notre double boucle :
wei = torch.tril(torch.ones(T, T))
wei = wei / wei.sum(1, keepdim=True)
xbow2 = wei @ x # (B, T, T) @ (B, T, C) ----> (B, T, C) fonctionne grâce au broadcasting de pytorch
torch.allclose(xbow, xbow2) # Vérifie que tous les éléments sont identiques
True
À la place de la normalisation, on peut utiliser la fonction softmax.
tril = torch.tril(torch.ones(T, T))
wei = torch.zeros((T,T))
# On met toutes les valeurs égales à 0 à la valeur -inf
wei = wei.masked_fill(tril == 0, float('-inf'))
print(wei)
tensor([[0., -inf, -inf, -inf],
[0., 0., -inf, -inf],
[0., 0., 0., -inf],
[0., 0., 0., 0.]])
On peut maintenant appliquer la softmax sur la matrice et TADAAA :
wei = F.softmax(wei, dim=-1)
print(wei)
xbow3 = wei @ x
torch.allclose(xbow, xbow3)
tensor([[1.0000, 0.0000, 0.0000, 0.0000],
[0.5000, 0.5000, 0.0000, 0.0000],
[0.3333, 0.3333, 0.3333, 0.0000],
[0.2500, 0.2500, 0.2500, 0.2500]])
True
En pratique, la version avec softmax est utilisée pour la couche self-attention.
Self-Attention : le cœur du transformer#
Actuellement, la matrice \(wei\) contient des valeurs uniformes sur chaque ligne, ce qui ne donne aucune information réelle sur l’importance des informations précédentes.
C’est là que le concept de self-attention intervient. Ce qu’on veut, c’est une matrice \(wei\) qu’on peut entraîner.
On va créer 3 valeurs à partir de notre valeur \(x\) :
query : Qu’est-ce que je recherche ? Cette valeur représente ce que chaque position de la séquence essaie de trouver dans les autres positions.
key : Qu’est-ce que je contiens ? Cette valeur représente ce que chaque position de la séquence contient comme information, qui pourrait être pertinente pour d’autres positions.
value : Quelle est ma valeur ? Cette valeur représente l’information réelle à extraire de chaque position de la séquence, si elle est jugée pertinente.
Pour extraire les valeurs query, key et value, on utilise une couche linéaire qui projette l’entrée dans une dimension head_size.
Pour calculer l’importance d’un élément précédent de la séquence par rapport à l’élément actuel, on effectue le produit scalaire entre les query \(Q\) et les key \(K\) (transposée) :
\(wei = QK^T\)
Pour obtenir des poids d’attention (somme égale à 1), on applique la softmax et on multiplie par les value \(V\) :
\(Output = \text{softmax}\left(wei\right) \cdot V\)
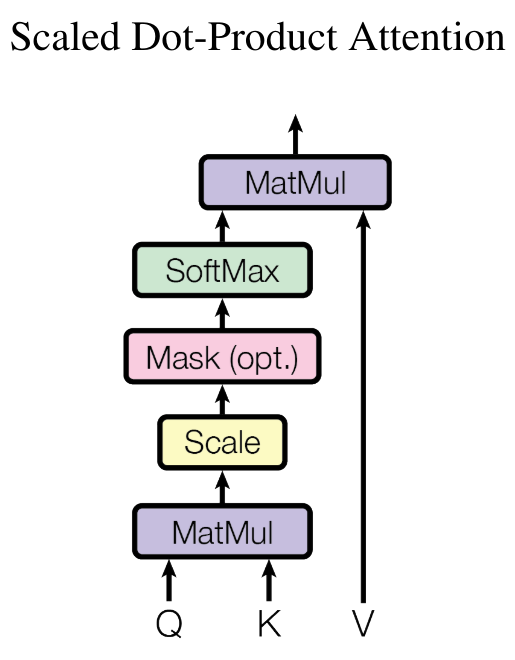
En Python, on l’implémente de cette manière :
B,T,C = 4,8,32 # batch, time, channels
x = torch.randn(B,T,C)
head_size = 16 # Valeur de head_size (projection de x)
key = nn.Linear(C, head_size, bias=False)
query = nn.Linear(C, head_size, bias=False)
value = nn.Linear(C, head_size, bias=False)
k = key(x) # (B, T, 16)
q = query(x) # (B, T, 16)
wei = q @ k.transpose(-2, -1) # (B, T, 16) @ (B, 16, T) ---> (B, T, T)
tril = torch.tril(torch.ones(T, T))
wei = wei.masked_fill(tril == 0, float('-inf')) # Pour appliquer le softmax, il faut des valeurs -inf
wei = F.softmax(wei, dim=-1)
v = value(x)
out = wei @ v
out.shape
torch.Size([4, 8, 16])
Notre matrice \(wei\) est donc maintenant entièrement entraînable, et il est possible d’utiliser cette couche pour entraîner un réseau de neurones.
Notes sur la couche self-attention :
L’attention est un mécanisme de communication qui peut être vu comme un graphe avec des connexions entre les nœuds (dans notre cas, les nœuds de fin sont connectés à l’ensemble des nœuds précédents).
Dans la couche d’attention, il n’y a aucune notion de la position des éléments les uns par rapport aux autres. Pour combler ce problème, il faudra ajouter un positionnal_embedding (voir suite du cours).
Pour précision, il n’y a aucune interaction le long de la dimension batch : chaque élément du batch est traité indépendamment des autres. C’est un peu comme si on avait batch_size graphes indépendants.
Ce block d’attention est appelé decoder block. Il a la particularité que chaque élément ne communique qu’avec le passé (grâce à la matrice triangulaire inférieure). Cependant, il existe d’autres couches d’attention (encoder) qui permettent la communication de tous les éléments les uns avec les autres (pour la traduction, l’analyse de sentiments ou encore le traitement d’images).
On parle de self-attention car les query, key et value viennent de la même source. Il est possible d’avoir des query, key et value qui proviennent de sources différentes : on parle alors de cross-attention.
Si vous lisez le papier Attention is all you need, vous constaterez qu’il y a une normalisation par la racine de la head_size :

Cela permet une stabilité de la fonction softmax lors de l’initialisation des poids en particulier.
Implémentons maintenant une classe head qui va effectuer les opérations de la self-attention. C’est simplement ce qu’on a vu précédemment sous forme de classe.
class Head(nn.Module):
""" Couche de self-attention unique """
def __init__(self, head_size,n_embd,dropout=0.2):
super().__init__()
self.key = nn.Linear(n_embd, head_size, bias=False)
self.query = nn.Linear(n_embd, head_size, bias=False)
self.value = nn.Linear(n_embd, head_size, bias=False)
self.register_buffer('tril', torch.tril(torch.ones(block_size, block_size)))
# Ajout de dropout pour la regularization
self.dropout = nn.Dropout(dropout)
def forward(self, x):
B,T,C = x.shape
k = self.key(x) # (B,T,C)
q = self.query(x) # (B,T,C)
# Le * C**-0.5 correspond à la normalisation par la racine de head_size
wei = q @ k.transpose(-2,-1) * C**-0.5 # (B, T, C) @ (B, C, T) -> (B, T, T)
wei = wei.masked_fill(self.tril[:T, :T] == 0, float('-inf')) # (B, T, T)
wei = F.softmax(wei, dim=-1) # (B, T, T)
wei = self.dropout(wei)
v = self.value(x) # (B,T,C)
out = wei @ v # (B, T, T) @ (B, T, C) -> (B, T, C)
return out
Multi-Head Attention#
Dans Attention is all you need (Vaswani et al., 2017), le multi-head attention étend la self-attention en calculant plusieurs représentations d’attention en parallèle (les “têtes”). Chaque tête apprend à capturer des dépendances spécifiques (syntaxiques, sémantiques, locales, etc.), ce qui enrichit la représentation des données. Ce mécanisme enrichit la représentation des données et tire parti du parallélisme des GPU.
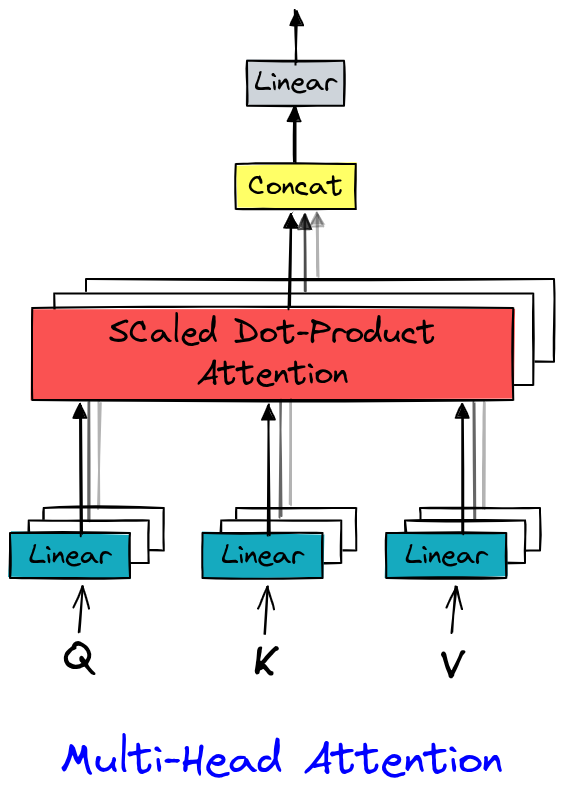
L’implémentation est assez simple puisqu’il s’agit juste de plusieurs couches head.
class MultiHeadAttention(nn.Module):
""" Plusieurs couches de self attention en parallèle"""
def __init__(self, num_heads, head_size,n_embd,dropout):
super().__init__()
# Création de num_head couches head de taille head_size
self.heads = nn.ModuleList([Head(head_size) for _ in range(num_heads)])
# Couche pour Linear (voir schema) après concatenation
self.proj = nn.Linear(n_embd, n_embd)
# Dropout si besoin
self.dropout = nn.Dropout(dropout)
def forward(self, x):
out = torch.cat([h(x) for h in self.heads], dim=-1)
out = self.dropout(self.proj(out))
return out
Feed Forward layer#
Un dernier élément du transformer qu’on peut voir dans le papier Attention is all you need est la couche Feed Forward, qui est simplement un petit réseau fully connected.
On l’implémente en Python comme cela :
class FeedFoward(nn.Module):
def __init__(self, n_embd,dropout):
super().__init__()
self.net = nn.Sequential(
# 4*n_embd comme dans le papier
nn.Linear(n_embd, 4 * n_embd),
nn.ReLU(),
nn.Linear(4 * n_embd, n_embd),
nn.Dropout(dropout),
)
def forward(self, x):
return self.net(x)
Couche transformer#
On a maintenant tous les éléments pour implémenter notre couche transformer, qui va utiliser multi-head attention et feed forward. Sur la figure principale du papier, on remarque aussi qu’il y a des connexions résiduelles entre l’input et l’output des couches d’attention et de feed forward. Ces connexions facilitent l’entraînement d’un modèle profond (plus de détails dans le papier Deep Residual Learning for Image Recognition). On va donc aussi implémenter ces connexions résiduelles. Pour la layer norm, on ne va pas entrer dans les détails ici, mais on peut comparer son utilité à une couche de batch norm (plus de détails dans ce blogpost). On utilise donc simplement l’implémentation PyTorch de la layer norm.
Voici l’implémentation Python :
class TransformerBlock(nn.Module):
""" Block transformer"""
def __init__(self, n_embd, n_head):
super().__init__()
head_size = n_embd // n_head
self.sa = MultiHeadAttention(n_head, head_size)
self.ffwd = FeedFoward(n_embd)
self.ln1 = nn.LayerNorm(n_embd)
self.ln2 = nn.LayerNorm(n_embd)
def forward(self, x):
x = x + self.sa(self.ln1(x)) # x+ car c'est une connexion résiduelle
x = x + self.ffwd(self.ln2(x))
return x
Note : On applique la layer norm avant les couches (contrairement au papier). C’est la seule partie du transformer qui a été modifiée depuis la publication du papier, et qui améliore les performances.
Pour plus de clarté, on va créer notre modèle et l’optimiser dans le notebook suivant.