Réseaux de neurones récurrents

Réseaux de neurones récurrents#

Dans ce cours, on va découvrir les réseaux de neurones récurrents (RNN) pour prédire le prochain caractère. On se base sur l’architecture décrite dans l’article Recurrent neural network based language model, qui propose une version simple de RNN pour cette tâche.

L’avantage des RNN est qu’ils n’ont pas besoin d’une taille de contexte fixe, contrairement aux modèles basés sur des réseaux fully connected vus précédemment.

Les RNN gardent en mémoire le contexte, quelle que soit la longueur de la séquence. C’est une idée cool en théorie, mais on verra à la fin du cours qu’ils ont leurs limites.

RNN

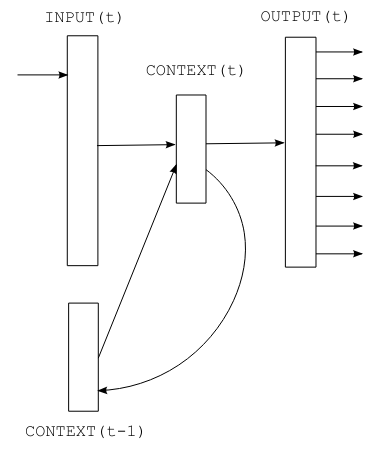
Figure extraite de l’article original.

Comment fonctionne un RNN ?#

Les RNN fonctionnent de manière séquentielle : les caractères sont traités un par un. Le caractère suivant dépend à la fois de l’élément actuel et de l’état (state) mémorisé, qui contient les infos des caractères précédents.

Mathématiquement, un RNN a 3 composantes :

  • L’entrée (input) \(x\)

  • L’état caché (state) \(s\)

  • La sortie (output) \(y\)

On ajoute aussi le temps \(t\) pour gérer la séquence.

L’entrée à l’instant \(t\) est donnée par : \(x(t) = w(t) + s(t-1)\) où \(w()\) est l’encodage one-hot et \(s(t-1)\) est l’état précédent.

Ensuite, on calcule l’état et la sortie : \(s(t) = sigmoid(x(t))\) \(y(t) = softmax(s(t))\)

Le seul paramètre à ajuster est la taille de la couche cachée \(s\).

Pour l’initialisation, \(s(0)\) peut être un petit vecteur.

Passage à la pratique#

import torch
import torch.nn as nn

Le dataset#

Générer des prénoms avec un RNN n’est pas super utile, car les prénoms sont courts et le contexte limité. Pour des tâches plus intéressantes, on a besoin d’un dataset avec un contexte plus large.

On utilise donc un fichier texte contenant les dialogues de Molière. Ce dataset a été créé à partir des œuvres complètes disponibles sur Gutenberg.org. J’ai nettoyé les données pour ne garder que les dialogues.

with open('moliere.txt', 'r', encoding='utf-8') as f:
    text = f.read()
print("Nombre de caractères dans le dataset : ", len(text))

Nombre de caractères dans le dataset :  1687290

Comme le dataset est volumineux, on prend seulement une partie (par exemple les 50 000 premiers caractères) pour un traitement plus rapide.

text=text[:50000]
print("Nombre de caractères dans le dataset : ", len(text))

Nombre de caractères dans le dataset :  50000

Voici les 250 premiers caractères :

print(text[:250])

VALÈRE.

Eh bien, Sabine, quel conseil me donnes-tu?

SABINE.

Vraiment, il y a bien des nouvelles. Mon oncle veut résolûment que ma
cousine épouse Villebrequin, et les affaires sont tellement avancées,
que je crois qu'ils eussent été mariés dès aujo

Voici le nombre de caractères uniques :

chars = sorted(list(set(text)))
vocab_size = len(chars)
print(''.join(chars))
print("Nombre de caractères différents : ", vocab_size)

 !'(),-.:;?ABCDEFGHIJLMNOPQRSTUVYabcdefghijlmnopqrstuvxyzÇÈÉàâæçèéêîïôùû
Nombre de caractères différents :  73

On crée un mapping entre caractères et entiers (et inversement)

stoi = { ch:i for i,ch in enumerate(chars) }
itos = { i:ch for i,ch in enumerate(chars) }
encode = lambda s: [stoi[c] for c in s] # encode : prend un string et output une liste d'entiers
decode = lambda l: ''.join([itos[i] for i in l]) # decode: prend une liste d'entiers et output un string

On encode le dataset en convertissant les chaînes de caractères en entiers, puis en tenseurs PyTorch.

data = torch.tensor(encode(text), dtype=torch.long)
print(data[:250]) # Les 250 premiers caractères encodé

tensor([32, 12, 22, 59, 28, 16,  8,  0,  0, 16, 41,  1, 35, 42, 38, 46,  6,  1,
        29, 34, 35, 42, 46, 38,  6,  1, 49, 53, 38, 44,  1, 36, 47, 46, 51, 38,
        42, 44,  1, 45, 38,  1, 37, 47, 46, 46, 38, 51,  7, 52, 53, 11,  0,  0,
        29, 12, 13, 20, 24, 16,  8,  0,  0, 32, 50, 34, 42, 45, 38, 46, 52,  6,
         1, 42, 44,  1, 56,  1, 34,  1, 35, 42, 38, 46,  1, 37, 38, 51,  1, 46,
        47, 53, 54, 38, 44, 44, 38, 51,  8,  1, 23, 47, 46,  1, 47, 46, 36, 44,
        38,  1, 54, 38, 53, 52,  1, 50, 66, 51, 47, 44, 72, 45, 38, 46, 52,  1,
        49, 53, 38,  1, 45, 34,  0, 36, 47, 53, 51, 42, 46, 38,  1, 66, 48, 47,
        53, 51, 38,  1, 32, 42, 44, 44, 38, 35, 50, 38, 49, 53, 42, 46,  6,  1,
        38, 52,  1, 44, 38, 51,  1, 34, 39, 39, 34, 42, 50, 38, 51,  1, 51, 47,
        46, 52,  1, 52, 38, 44, 44, 38, 45, 38, 46, 52,  1, 34, 54, 34, 46, 36,
        66, 38, 51,  6,  0, 49, 53, 38,  1, 43, 38,  1, 36, 50, 47, 42, 51,  1,
        49, 53,  3, 42, 44, 51,  1, 38, 53, 51, 51, 38, 46, 52,  1, 66, 52, 66,
         1, 45, 34, 50, 42, 66, 51,  1, 37, 65, 51,  1, 34, 53, 43, 47])

On sépare les données en ensembles d’entraînement et de test :

n = int(0.9*len(data)) # 90% pour le train et 10% pour le test
train_data = data[:n]
test = data[n:]

Note : À chaque itération, on parcourt tout le dataset de manière séquentielle.

Construction du modèle#

On va maintenant construire le modèle !

Comme indiqué dans l’article, l’entrée (le caractère) est encodée en one-hot, puis additionnée avec l’état précédent. On a donc besoin de deux couches fully connected :

  • La première transforme l’entrée \(x(t)\) en état \(s(t)\)

  • La seconde transforme \(s(t)\) en prédiction \(y(t)\)

RNN

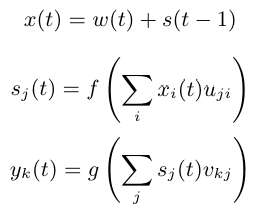
Équation tirée de l’article. \(f\) est la fonction sigmoid et \(g\) la softmax.

Note : L’article est clair et concis, je vous conseille de le lire.

class rnn(nn.Module): 
  def __init__(self,hidden_dim,vocab_size) -> None:
    super(rnn, self).__init__()
    self.hidden_to_hidden=nn.Linear(hidden_dim+vocab_size, hidden_dim)
    self.hidden_to_output=nn.Linear(hidden_dim, vocab_size)
    self.vocab_size=vocab_size
    self.hidden_dim=hidden_dim
    self.sigmoid=nn.Sigmoid() 
    
  # Le réseau prend en entrée le caractère actuel et le state précédent
  def forward(self, x,state):
    # On one-hot encode le caractère
    x = torch.nn.functional.one_hot(x, self.vocab_size).float()
    if state is None:
      # Si on a pas de state (début de la séquence), on initialise le state avec des petites valeurs aléatoires
      state = torch.randn(self.hidden_dim) * 0.1
    x = torch.cat((x, state), dim=-1)  # Concaténation de x et du state
    state = self.sigmoid(self.hidden_to_hidden(x)) # Calcul du nouveau state
    output = self.hidden_to_output(state) # Calcul de l'output
    # On renvoie l'output et le state pour le prochain pas de temps
    return output, state.detach() # detach() pour éviter de propager le gradient dans le state

Entraînement du modèle#

Voici les paramètres d’entraînement :

epochs = 10
lr=0.1
hidden_dim=128
model=rnn(hidden_dim,vocab_size)
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=lr)

On entraîne maintenant le modèle !

for epoch in range(epochs):
    state=None
    running_loss = 0
    n=0
    for i in range(len(train_data)-1):
        x = train_data[i]
        y = train_data[i+1]
        optimizer.zero_grad()
        y_pred,state = model.forward(x,state)
        loss = criterion(y_pred, y)
        running_loss += loss.item()
        n+=1
        loss.backward()
        optimizer.step()

    print("Epoch: {0} \t Loss: {1:.8f}".format(epoch, running_loss/n))

Epoch: 0 	 Loss: 2.63949568
Epoch: 1 	 Loss: 2.16456994
Epoch: 2 	 Loss: 2.00850788
Epoch: 3 	 Loss: 1.91673251
Epoch: 4 	 Loss: 1.84440742
Epoch: 5 	 Loss: 1.78986003
Epoch: 6 	 Loss: 1.74923073
Epoch: 7 	 Loss: 1.71709289
Epoch: 8 	 Loss: 1.68791167
Epoch: 9 	 Loss: 1.66215199

On teste maintenant le modèle sur les données de test :

state=None
running_loss = 0
n=0
for i in range(len(train_data)-1):
    with torch.no_grad():
        x = train_data[i]
        y = train_data[i+1]
        y_pred,state = model.forward(x,state)
        loss = criterion(y_pred, y)
        running_loss += loss.item()
        n+=1
print("Loss: {0:.8f}".format(running_loss/n))

Loss: 1.77312289

Le loss sur les données de test est légèrement plus élevé qu’en entraînement. Le modèle a un peu overfitté.

Génération de texte#

Le modèle étant entraîné, on peut maintenant générer du texte façon Molière !

import torch.nn.functional as F 
moliere='.'
sequence_length=250
state=None
for i in range(sequence_length):
    x = torch.tensor(encode(moliere[-1]), dtype=torch.long).squeeze()
    y_pred,state = model.forward(x,state)
    probs=F.softmax(torch.squeeze(y_pred), dim=0)
    sample=torch.multinomial(probs, 1)
    moliere+=itos[sample.item()]
print(moliere)

.

VARDILE.

Vout on est nt, jes l'un ouint; sabhil.

LE DOCTE.

Si vous dicefalassîntes
GIRGIB.

MARGRIILÉ.

LE DOCTE. Jort; et
; bieu,
et je mu tu d'ais d'ai coupce!

SGÉLLÉ.

Il Sgnous elli massit que
Suis pluagil dés.
Cais téscompas: y totte demes

Le résultat n’est pas parfait, mais on reconnaît quelques mots et une structure de phrases proche du fichier “moliere.txt”. Pas mal pour un RNN à une seule couche !

Comment améliorer les résultats ? Voici quelques pistes :

  • Augmenter le nombre de couches ou la taille de la couche cachée

  • Utiliser un embedding au lieu du one-hot encoding

  • Tester d’autres variantes de RNN comme LSTM ou GRU

  • ~~Utiliser une architecture transformer~~ (spoiler !)

Les limites des RNN#

Longtemps au cœur de la recherche en NLP et en deep learning, les RNN ont plusieurs limites qui les rendent peu pratiques pour les gros modèles :

  • Leur architecture permet un contexte infini en théorie, mais la structure séquentielle complique la propagation de l’info sur de longues séquences.

  • Le vanishing gradient sur les longues séquences est un vrai problème.

  • La structure séquentielle rend la parallélisation difficile, alors que les GPU sont optimisés pour les calculs parallèles. L’entraînement est donc plus lent.

  • La structure fixe n’est pas toujours adaptée pour capturer les relations complexes.

Depuis l’arrivée des transformers, les RNN sont de moins en moins utilisés.

Contents