Autoencodeurs variationnels#
Dans ce cours, on te présente les autoencodeurs variationnels, aussi appelés variational autoencoders (VAE). On commence par un petit rappel du cours 4 sur les autoencodeurs, puis on introduit l’utilisation des VAE comme modèle génératif. Ce cours s’inspire d’un blogpost et ne rentre pas dans les détails maths du fonctionnement du VAE. Les figures utilisées dans ce notebook viennent aussi du blogpost.
Rappel sur les autoencodeurs#
Un autoencodeur, c’est un réseau de neurones en forme de sablier. Il est composé d’un encodeur qui encode l’info dans un espace latent de dimension réduite et d’un décodeur qui reconstruit la donnée initiale à partir de la représentation latente.
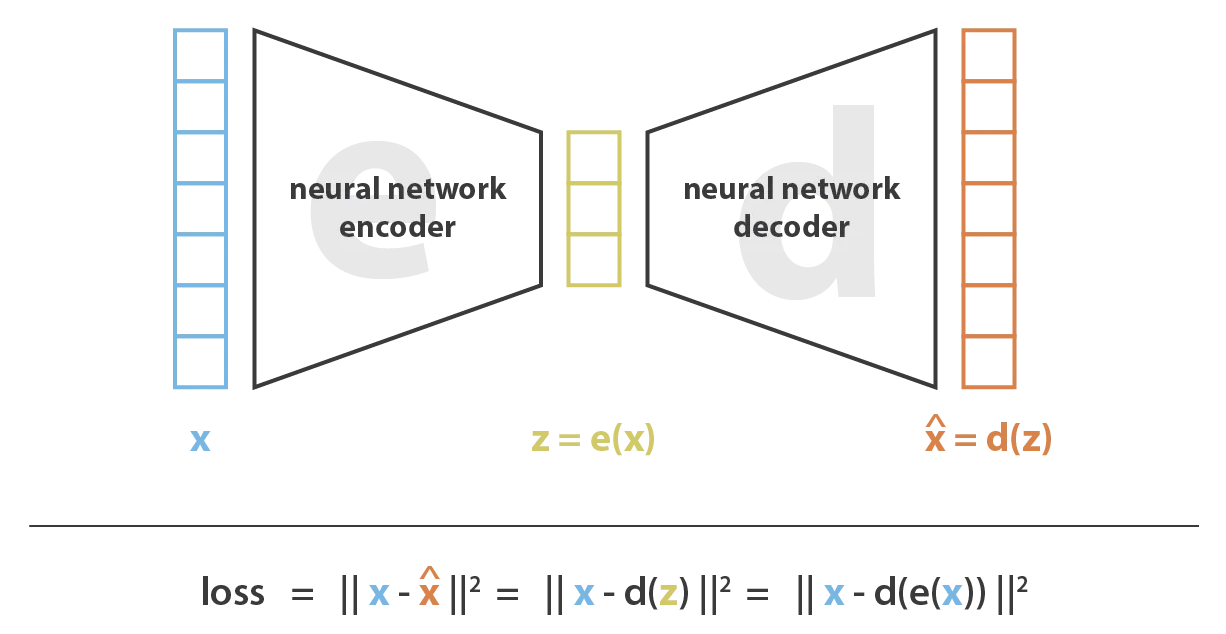
Les autoencodeurs peuvent servir à plein de choses, mais leur rôle de base, c’est la compression de données. C’est une méthode de compression qui utilise l’optimisation par descente de gradient.
Intuition#
Imagine que l’espace latent de notre décodeur est régulier (représenté par une distribution de probabilité connue). Dans ce cas, on pourrait sampler un élément aléatoire de cette distribution pour générer une nouvelle donnée. En pratique, dans un autoencodeur classique, la représentation latente n’est pas régulière, donc impossible à utiliser pour générer des données.
En y réfléchissant, c’est logique. La fonction de loss de l’autoencodeur se base uniquement sur la qualité de la reconstruction et n’impose aucune contrainte sur la forme de l’espace latent.
Du coup, on aimerait bien imposer la forme de l’espace latent de notre autoencodeur pour générer des nouvelles données à partir de cet espace latent.
Autoencodeur variationnel#
Un variational autoencoder (VAE), c’est un autoencodeur contraint à avoir un espace latent qui permet de générer des données. Il a un entraînement régulé pour cet objectif.
L’idée, c’est d’encoder notre input en une distribution de données au lieu d’une simple valeur (comme dans un AE). En pratique, notre encodeur va prédire deux valeurs représentant une distribution normale : la moyenne \(\mu\) et la variance \(\sigma^2\).
Le VAE fonctionne comme ça pendant l’entraînement :
L’encodeur encode l’input en une distribution de probabilité en prédisant \(\mu\) et \(\sigma^2\).
Une valeur est sampled à partir de la distribution gaussienne décrite par \(\mu\) et \(\sigma^2\).
Le décodeur reconstruit la donnée à partir de la valeur sampled.
On applique la backpropagation pour mettre à jour les poids.
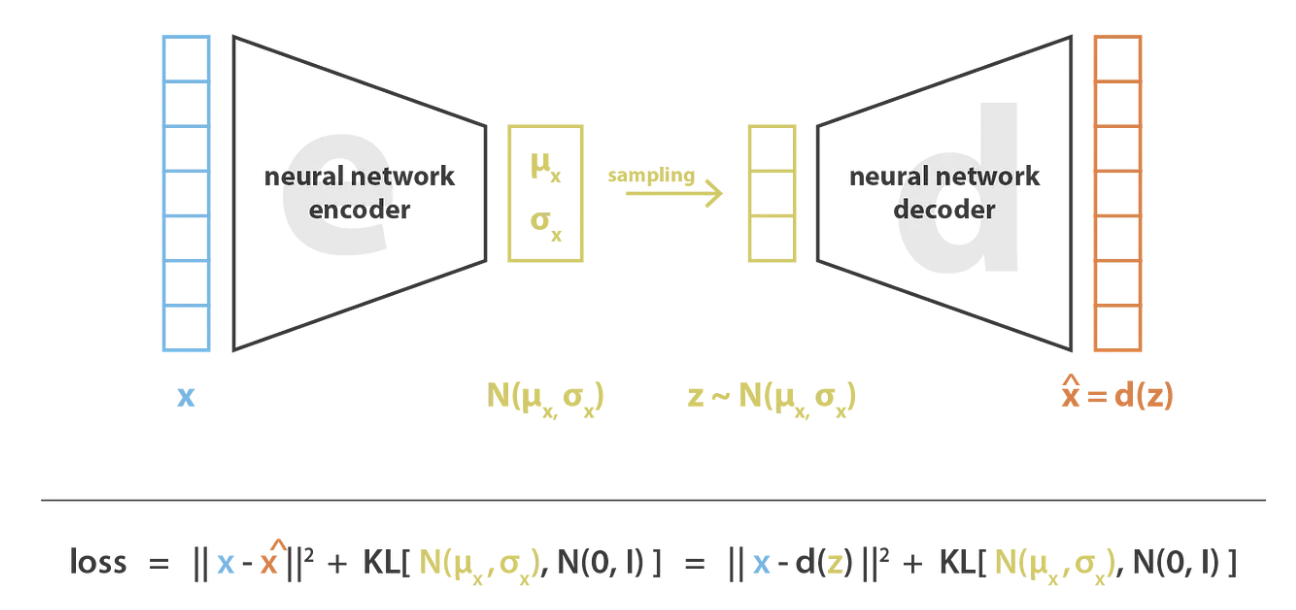
Pour garantir que l’entraînement fait bien ce qu’on veut, il faut ajouter un terme à la fonction de loss : la divergence de Kullback-Leibler. Ce terme permet de pousser la distribution à être une distribution centrée réduite.
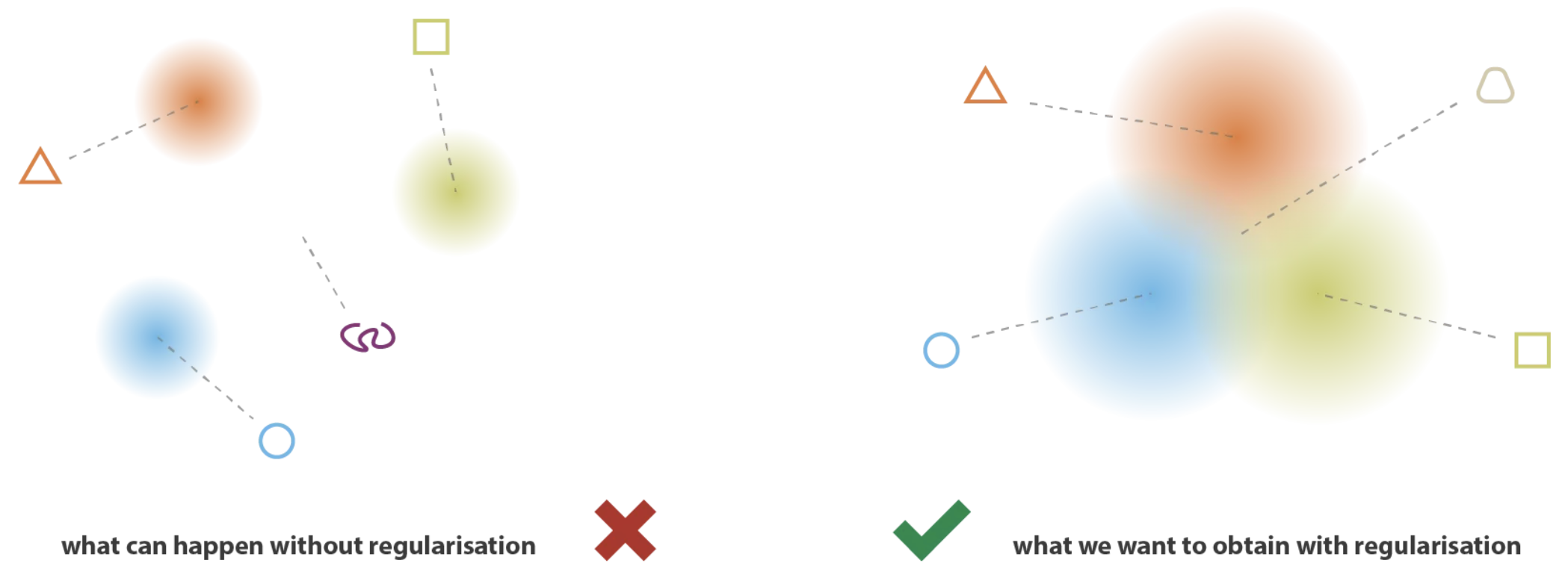
Pour avoir une génération de données cohérentes, il y a deux choses à prendre en compte :
La continuité : Des points proches dans l’espace latent vont produire des données proches dans l’espace de sortie.
La complétude : Les points décodés doivent avoir du sens dans l’espace de sortie.
La divergence de Kullback-Leibler permet de garantir ces deux propriétés. Si on se contentait du loss de reconstruction, le VAE pourrait se comporter comme un AE en prédisant des variances presque nulles (ce qui serait presque équivalent à un point, comme ce qu’on prédit avec un encodeur d’un AE).
La divergence de Kullback-Leibler encourage les distributions de l’espace latent à être proches les unes des autres. Ça permet de générer des données toujours cohérentes quand on sample.
Note : Il y a un aspect théorique important derrière les Variational autoencoders, mais on ne va pas rentrer dans les détails dans ce cours. Pour en apprendre plus, vous pouvez vous référer au cours CS236 de Stanford et en particulier à ce lien.