Mon premier réseau de neurones#
Dans ce cours, nous allons construire notre premier réseau de neurones en utilisant la bibliothèque micrograd. Micrograd est une bibliothèque simple et facile à comprendre, spécialisée dans le calcul automatique des gradients. Pour mieux la maîtriser, vous pouvez regarder la vidéo d’introduction d’Andrej Karpathy (en anglais). Ce notebook s’inspire également du notebook fourni dans le dépôt de micrograd.
Construction d’un réseau de neurones avec micrograd#
#!pip install micrograd # uncomment to install micrograd
import random
import numpy as np
import matplotlib.pyplot as plt
from micrograd.engine import Value
from micrograd.nn import Neuron, Layer, MLP
# Pour la reproducibilité
np.random.seed(1337)
random.seed(1337)
Pour construire un réseau de neurones, nous avons d’abord besoin d’un problème à résoudre. Nous utilisons pour cela la fonction make_moons de scikit-learn, qui permet de générer un dataset. Pour simplifier le calcul du loss dans les étapes suivantes, nous remplaçons les classes 0 et 1 par les classes -1 et 1.
Initialisation du dataset#
from sklearn.datasets import make_moons, make_blobs
X, y = make_moons(n_samples=100, noise=0.1) # 100 éléments et un bruit Gaussien d'écart type 0.1 ajouté sur les données
print("Les données d'entrée sont de la forme : ",X[1])
y = y*2 - 1 # Pour avoir y=-1 ou y=1 (au lieu de 0 et 1)
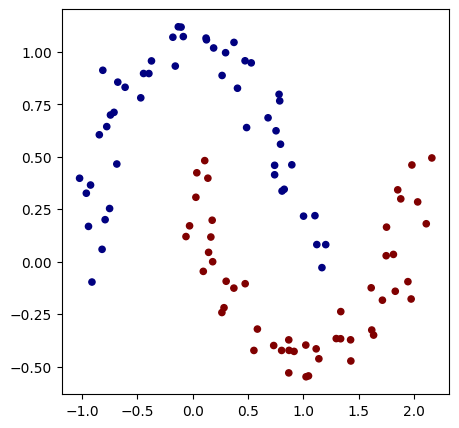
# Visualisation des données en 2D
plt.figure(figsize=(5,5))
plt.scatter(X[:,0], X[:,1], c=y, s=20, cmap='jet')
Les données d'entrée sont de la forme : [-0.81882941 0.05879006]
<matplotlib.collections.PathCollection at 0x177253e50>
Création du réseau de neurones#
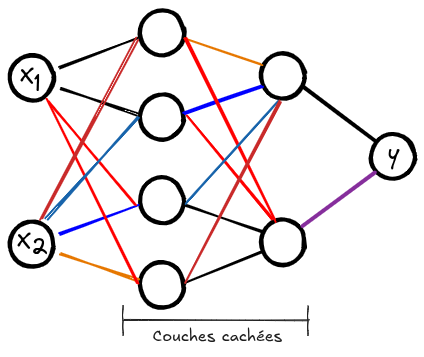
Maintenant, nous allons initialiser notre réseau de neurones. Celui-ci prend 2 valeurs en entrée et doit produire un label -1 ou 1. Le réseau que nous allons construire possède 2 couches cachées, chacune contenant 16 neurones. Chaque neurone fonctionne comme une régression logistique, ce qui fait de notre réseau un assemblage non linéaire de plusieurs régressions logistiques.
Voici un aperçu de l’architecture de ce réseau :
# Initialisation du modèle
model = MLP(2, [16, 16, 1]) # Couches d'entrée de taille 2, deux couches cachées de 16 neurones et un neurone de sortie
print(model)
print("Nombre de paramètres", len(model.parameters()))
MLP of [Layer of [ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2)], Layer of [ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16)], Layer of [LinearNeuron(16)]]
Nombre de paramètres 337
Descente de gradient stochastique (SGD)#
Avant de continuer, faisons un point sur la descente de gradient stochastique (SGD). Pour appliquer l’algorithme de descente de gradient sur un dataset de taille \(N\), il faudrait en théorie calculer la perte et le gradient sur chaque élément avant de mettre à jour les poids. Cette méthode garantit une diminution de la perte à chaque itération, mais elle est très coûteuse pour des datasets où \(N\) est grand (souvent \(N>10⁶\)). De plus, il faudrait stocker les gradients de tous les \(N\) éléments en mémoire, ce qui est impossible pour de grands ensembles de données.
Pour résoudre ce problème, nous utilisons des mini-batch, qui sont des groupes d’échantillons du dataset. L’optimisation se fait comme pour la descente de gradient classique, mais la mise à jour des poids se fait à chaque mini-batch (donc plus fréquemment). Cela rend le processus d’optimisation plus rapide et permet de traiter de grandes quantités de données. La taille d’un mini-batch est appelée batch size et sa valeur est souvent 16, 32 ou 64. Pour en savoir plus sur la descente de gradient stochastique, consultez Wikipedia ou ce blogpost.
Définissons en Python une fonction pour récupérer batch_size éléments aléatoires de notre dataset.
def get_batch(batch_size=64):
ri = np.random.permutation(X.shape[0])[:batch_size]
Xb, labels = X[ri], y[ri]
#inputs = [list(map(Value, xrow)) for xrow in Xb] # OLD
# Conversion des inputs en Value pour pouvoir utiliser micrograd
inputs = [list([Value(xrow[0]),Value(xrow[1])]) for xrow in Xb]
return inputs,labels
Fonction de perte#
Pour entraîner notre réseau de neurones, nous devons définir une fonction de perte (loss). Dans notre cas, nous avons deux classes et nous voulons maximiser la marge entre les exemples appartenant à des classes différentes. Contrairement à la perte de log-vraisemblance négative utilisée précédemment, nous cherchons à maximiser cet écart, ce qui rend notre méthode plus robuste aux nouveaux éléments.
Nous utilisons le loss max-margin (marge maximale), défini par : \(\text{loss} = \max(0, 1 - y_i \cdot \text{score}_i)\)
def loss_function(scores,labels):
# La fonction .relu() prend le maximum entre 0 et la valeur de 1 - yi*scorei
losses = [(1 - yi*scorei).relu() for yi, scorei in zip(labels, scores)]
# On divise le loss par le nombre d'éléments du mini-batch
data_loss = sum(losses) * (1.0 / len(losses))
return data_loss
Entraînement du modèle#
Maintenant que nous avons les éléments clés de l’entraînement, il est temps de définir notre boucle d’entraînement
# Définissons nos hyper-paramètres d'entraînement
batch_size=128
iteration=50
On peut maintenant lancer l’entraînement de notre modèle :
for k in range(iteration):
# On récupère notre mini-batch random
inputs,labels=get_batch(batch_size=batch_size)
# On fait appel au modèle pour calculer les scores Y
scores = list(map(model, inputs))
# On calcule le loss
loss=loss_function(scores,labels)
accuracy = [(label > 0) == (scorei.data > 0) for label, scorei in zip(labels, scores)]
accuracy=sum(accuracy) / len(accuracy)
# Remise à zéro de valeurs de gradients avant de les calculer
model.zero_grad()
# Calcul des gradients grâce à l'autograd de micrograd
loss.backward()
# Mise à jour des poids avec les gradients calculés (SGD)
learning_rate = 1.0 - 0.9*k/100 # On diminue le learning rate au fur et à mesure de l'entraînement
for p in model.parameters():
p.data -= learning_rate * p.grad
if k % 1 == 0:
print(f"step {k} loss {loss.data}, accuracy {accuracy*100}%")
step 0 loss 0.8862514464368221, accuracy 50.0%
step 1 loss 1.7136790633950052, accuracy 81.0%
step 2 loss 0.733396126728699, accuracy 77.0%
step 3 loss 0.7615247055858604, accuracy 82.0%
step 4 loss 0.35978083334534205, accuracy 84.0%
step 5 loss 0.3039360355411295, accuracy 86.0%
step 6 loss 0.2716587340549048, accuracy 89.0%
step 7 loss 0.25896576803013205, accuracy 91.0%
step 8 loss 0.2468445503533517, accuracy 91.0%
step 9 loss 0.26038987927745966, accuracy 91.0%
step 10 loss 0.23569710047306525, accuracy 91.0%
step 11 loss 0.2403768930229477, accuracy 92.0%
step 12 loss 0.20603128479123115, accuracy 91.0%
step 13 loss 0.22061157796029193, accuracy 93.0%
step 14 loss 0.19010711228374735, accuracy 92.0%
step 15 loss 0.21687609382796402, accuracy 93.0%
step 16 loss 0.18642445342175254, accuracy 92.0%
step 17 loss 0.2064478196088666, accuracy 92.0%
step 18 loss 0.15299793102189654, accuracy 94.0%
step 19 loss 0.18164592701596197, accuracy 93.0%
step 20 loss 0.15209012673698674, accuracy 92.0%
step 21 loss 0.17985784886850317, accuracy 93.0%
step 22 loss 0.13186703020683818, accuracy 95.0%
step 23 loss 0.13971668862318976, accuracy 95.0%
step 24 loss 0.1052987732627048, accuracy 96.0%
step 25 loss 0.11575214222251122, accuracy 95.0%
step 26 loss 0.10138692709798285, accuracy 97.0%
step 27 loss 0.13983249990522056, accuracy 95.0%
step 28 loss 0.13439433831552547, accuracy 92.0%
step 29 loss 0.14946491199753797, accuracy 95.0%
step 30 loss 0.08058651087395295, accuracy 97.0%
step 31 loss 0.08894402478347964, accuracy 97.0%
step 32 loss 0.14846171628770516, accuracy 95.0%
step 33 loss 0.08534324122933533, accuracy 97.0%
step 34 loss 0.06930425973662234, accuracy 97.0%
step 35 loss 0.10224309625633382, accuracy 95.0%
step 36 loss 0.05690038135075194, accuracy 97.0%
step 37 loss 0.04361190103707672, accuracy 97.0%
step 38 loss 0.04085954349889362, accuracy 98.0%
step 39 loss 0.06115860793647568, accuracy 97.0%
step 40 loss 0.06712605274368717, accuracy 99.0%
step 41 loss 0.1007776535938798, accuracy 95.0%
step 42 loss 0.047219615684323896, accuracy 97.0%
step 43 loss 0.03229533112572595, accuracy 99.0%
step 44 loss 0.028346610758982437, accuracy 99.0%
step 45 loss 0.05011775341000794, accuracy 99.0%
step 46 loss 0.09321634150737651, accuracy 96.0%
step 47 loss 0.055859575569553566, accuracy 98.0%
step 48 loss 0.02709965160774589, accuracy 99.0%
step 49 loss 0.054945465674614925, accuracy 98.0%
Comme vous pouvez le constater, le loss ne diminue pas systématiquement à chaque étape d’entraînement. Cela s’explique par la descente de gradient stochastique : le fait de ne pas prendre en compte l’ensemble des données à chaque itération introduit une part d’aléatoire. Cependant, le loss diminue en moyenne au cours de l’entraînement, ce qui permet d’obtenir un modèle robuste plus rapidement.
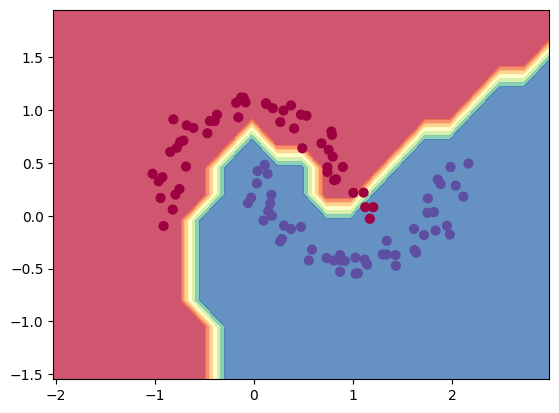
# Visualisation de la frontière de décision
h = 0.25
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Xmesh = np.c_[xx.ravel(), yy.ravel()]
inputs = [list(map(Value, xrow)) for xrow in Xmesh]
scores = list(map(model, inputs))
Z = np.array([s.data > 0 for s in scores])
Z = Z.reshape(xx.shape)
fig = plt.figure()
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
(-1.548639298268643, 1.951360701731357)