Autoencodeur pour le débruitage

Intuition

Qu’est-ce que le débruitage ?

Le débruitage consiste à éliminer le bruit indésirable d’une image. C’est une tâche cruciale en traitement d’images. Notre objectif est de fournir en entrée du réseau une image bruitée et d’obtenir en sortie une image nette.

Figure extraite de article.

Utilisation d’un autoencodeur pour le débruitage

Pour utiliser l’architecture de l’autoencodeur pour cette tâche, il suffit de fournir en entrée du décodeur une image bruitée (que nous avons générée), de lui faire reconstruire l’image et de comparer l’image reconstruite à l’image originale non bruitée.

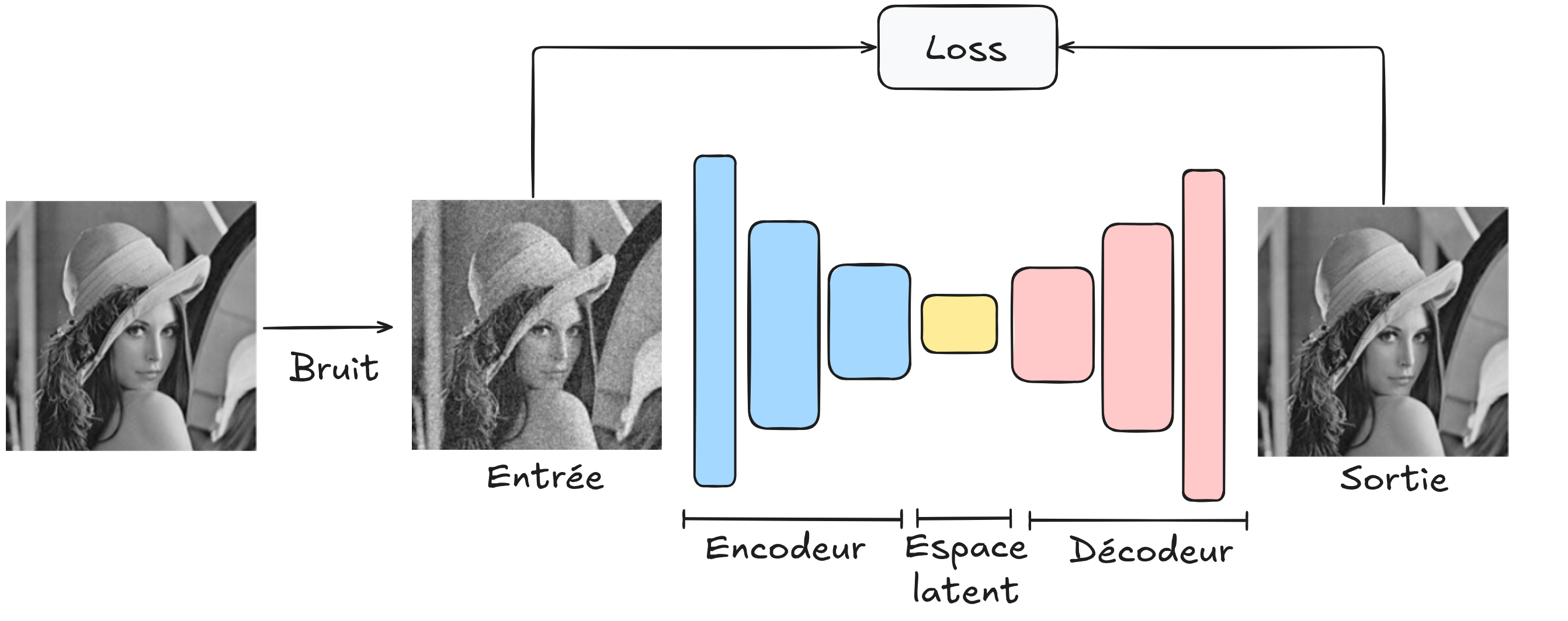
En utilisant cette architecture, nous cherchons à créer un modèle de débruitage robuste capable de débruiter toutes les images. Pour son entraînement, il faudra une grande base d’images et veiller à ce que le bruit généré soit similaire à celui que l’on rencontre sur des images réelles.

Débruitage avec un autoencodeur en PyTorch

Encore une fois, nous utilisons le dataset MNIST. Nous allons générer du bruit artificiel sur les images et entraîner notre autoencodeur à éliminer ce bruit pour obtenir une image nette.

import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision.transforms as T
from torchvision import datasets
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt

Dataset et dataloader

transform=T.ToTensor() # Pour convertir les éléments en tensor torch directement
dataset = datasets.MNIST(root='./../data', train=True, download=True,transform=transform)
test_dataset = datasets.MNIST(root='./../data', train=False,transform=transform)
train_dataset, validation_dataset=torch.utils.data.random_split(dataset, [0.8,0.2])
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
val_loader= DataLoader(validation_dataset, batch_size=64, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False)

Génération de bruit

Faisons un exemple d’application de bruit pour visualiser la dégradation de l’image en fonction du niveau de bruit.

image,_=dataset[0]
# Le paramètre dans le np.sqrt correspond à la variance désirée donc np.sqrt(...) est l'écart type
# torch.randn génére des valeurs aléatoire extraites d'une distribution gaussienne de mean 0 et variance 1
imageNoisy1 = image + np.sqrt(0.001)*torch.randn(1, 28, 28)
imageNoisy2 = image + np.sqrt(0.01)*torch.randn(1, 28, 28)
imageNoisy3 = image + np.sqrt(0.1)*torch.randn(1, 28, 28)

plt.subplot(2, 2, 1)
plt.imshow(image.squeeze().numpy(), cmap='gray')
plt.title("Image originale")

plt.subplot(2, 2, 2)
plt.imshow(imageNoisy1.squeeze().numpy(), cmap='gray')
plt.title("Faible bruit")

plt.subplot(2, 2, 3)
plt.imshow(imageNoisy2.squeeze().numpy(), cmap='gray')
plt.title("Bruit moyen")

plt.subplot(2, 2, 4)
plt.imshow(imageNoisy3.squeeze().numpy(), cmap='gray')
plt.title("Fort bruit")

plt.tight_layout()
plt.show()

Nous allons utiliser un niveau de bruit moyen lors de l’entraînement. Ensuite, nous pourrons observer comment notre autoencodeur de débruitage se comporte sur d’autres niveaux de bruit.

Création de notre modèle

Pour cette tâche complexe, nous utilisons un autoencodeur convolutif.

# Nous réutilisons les fonctions introduites dans l'exemple de segmentation du cours 3 
def conv_relu_bn(input_channels, output_channels, kernel_size, stride, padding):
  return nn.Sequential(
    nn.Conv2d(input_channels, output_channels, kernel_size, stride, padding),
    nn.ReLU(),
    nn.BatchNorm2d(output_channels,momentum=0.01)
  )
    
def convT_relu_bn(input_channels, output_channels, kernel_size, stride, padding):
  return nn.Sequential(
    nn.ConvTranspose2d(input_channels, output_channels, kernel_size, stride, padding),
    nn.ReLU(),
    nn.BatchNorm2d(output_channels,momentum=0.01)
  )
    
    
class ae_conv(nn.Module):
  def __init__(self, *args, **kwargs) -> None:
    super().__init__(*args, **kwargs)

    self.encoder = nn.Sequential( # Sequential permet de groupe une série de transformation
      conv_relu_bn(1,8,kernel_size=3,stride=2,padding=1),
      conv_relu_bn(8,16,kernel_size=3,stride=2,padding=1),
      conv_relu_bn(16,32,kernel_size=3,stride=1,padding=1),
    )
    self.decoder = nn.Sequential(
      convT_relu_bn(32,16,kernel_size=4,stride=2,padding=1),
      convT_relu_bn(16,8,kernel_size=4,stride=2,padding=1),
      nn.Conv2d(8,1,kernel_size=3,stride=1,padding=1),
      nn.Sigmoid()
    )
  
  def forward(self,x): 
    x = self.encoder(x)
    denoise = self.decoder(x)
    return denoise

model = ae_conv() # Couches d'entrée de taille 2, deux couches cachées de 16 neurones et un neurone de sortie
print("Nombre de paramètres", sum(p.numel() for p in model.parameters()))

Nombre de paramètres 16385

Entraînement du modèle

criterion = nn.MSELoss()
epochs=10
learning_rate=0.001
optimizer=torch.optim.Adam(model.parameters(),lr=learning_rate)

for i in range(epochs):
  loss_train=0
  for images, _ in train_loader:
    images=images+np.sqrt(0.01)*torch.randn(images.shape)
    recons=model(images)
    loss=criterion(recons,images)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    loss_train+=loss   
  if i % 1 == 0:
    print(f"step {i} train loss {loss_train/len(train_loader)}")
  loss_val=0    
  for images, _ in val_loader:
    with torch.no_grad():
      images=images+np.sqrt(0.01)*torch.randn(images.shape)
      recons=model(images)
      loss=criterion(recons,images)
      loss_val+=loss 
  if i % 1 == 0:
    print(f"step {i} val loss {loss_val/len(val_loader)}")

step 0 train loss 0.0253756046295166
step 0 val loss 0.010878251865506172
step 1 train loss 0.00976449716836214
step 1 val loss 0.008979358710348606
step 2 train loss 0.00827114749699831
step 2 val loss 0.007526080124080181
step 3 train loss 0.00706455297768116
step 3 val loss 0.0066648973152041435
step 4 train loss 0.006312613375484943
step 4 val loss 0.005955129396170378
step 5 train loss 0.00576859712600708
step 5 val loss 0.005603262223303318
step 6 train loss 0.0055686105042696
step 6 val loss 0.005487256217747927
step 7 train loss 0.0054872902110219
step 7 val loss 0.005444051697850227
step 8 train loss 0.0054359594359993935
step 8 val loss 0.005416598636657
step 9 train loss 0.005397486500442028
step 9 val loss 0.005359680857509375

images,_=next(iter(test_loader))
variance=0.01
#Isolons un élément
fig, axs = plt.subplots(2, 3, figsize=(10, 6)) 
for i in range(2):
  image=images[i].unsqueeze(0)
  noisy_image=image+np.sqrt(variance)*torch.randn(image.shape)

  with torch.no_grad():
      recons=model(noisy_image)

  # Image d'origine
  axs[i][0].imshow(noisy_image[0].squeeze().cpu().numpy(), cmap='gray')
  axs[i][0].set_title('Image d\'origine')
  axs[i][0].axis('off')

  # Image reconstruite
  axs[i][1].imshow(recons[0].squeeze().cpu().numpy(), cmap='gray')
  axs[i][1].set_title('Image reconstruite')
  axs[i][1].axis('off')

  axs[i][2].imshow(image[0].squeeze().cpu().numpy(), cmap='gray')
  axs[i][2].set_title('Image de base')
  axs[i][2].axis('off')
plt.show()

Les résultats de notre débruitage sont assez bons, bien qu’il reste quelques artefacts. En faisant varier le paramètre de variance, vous pouvez visualiser ce que l’autoencodeur de débruitage est capable de faire sur d’autres niveaux de bruit.

Exercice

Vous pouvez essayer d’entraîner le modèle sur des images avec un niveau de bruit aléatoire (compris entre certaines valeurs de variance) pour voir si le modèle est capable de généraliser à n’importe quel type de bruit gaussien dans cet intervalle. Vous pourriez avoir besoin de complexifier le modèle et d’ajouter des epochs lors de l’entraînement.

U-Net : Vous pouvez également essayer de tester l’architecture U-Net (voir cours 3 sur la segmentation) pour la tâche de débruitage et comparer les résultats avec l’autoencodeur.