Bigramme

Analyse du dataset

words = open('prenoms.txt', 'r').read().splitlines()
print('Les 5 prénoms les plus populaires : ',words[:5])
print('Les 5 prénoms les moins populaires : ',words[-5:])
print('Le prénom le plus long : ',max(words, key=len))
print('Le prénom le plus court : ',min(words, key=len))

Les 5 prénoms les plus populaires :  ['MARIE', 'JEAN', 'PIERRE', 'MICHEL', 'ANDRÉ']
Les 5 prénoms les moins populaires :  ['ÉLOUEN', 'CHEYNA', 'BLONDIE', 'IMANN', 'GHILAIN']
Le prénom le plus long :  GUILLAUME-ALEXANDRE
Le prénom le plus court :  GUY

unique_characters = set()
for word in words:
  # Ajouter chaque caractère de la ligne à l'ensemble des caractères uniques
  for char in word.strip():
    unique_characters.add(char)
print('Nombre de caractères uniques : ',len(unique_characters))
print('Caractères uniques : ',unique_characters)

Nombre de caractères uniques :  45
Caractères uniques :  {'Ï', 'Ü', 'Ÿ', 'U', 'Ô', 'S', 'Æ', 'À', 'È', '-', 'W', 'H', 'Ê', 'É', 'R', 'M', 'E', 'Ë', 'N', 'Î', 'X', 'Ä', 'F', 'Â', 'K', 'D', 'Ö', 'I', 'J', 'Y', 'A', 'C', 'O', 'Û', 'Ù', 'B', 'Z', 'P', 'T', "'", 'Q', 'Ç', 'G', 'L', 'V'}

Bigramme, qu’est-ce que c’est ?

Je rappelle que l’objectif du projet est de prédire le prochain caractère à partir des caractères précédents. Dans le modèle bigramme, on se base uniquement sur le caractère précédent pour prédire le caractère actuel. C’est la version la plus simple de ce type de modèle.

Bien sûr, pour prédire un prénom, on doit commencer par rien. Pour prédire la première lettre, on a besoin de connaître la probabilité qu’une lettre soit la première (et de même pour la dernière lettre). On ajoute donc un caractère spécial ‘.’ au début et à la fin de chaque mot avant de construire nos bigrammes.

Dans chaque prénom, on a plusieurs exemples de bigrammes (chacun est indépendant). Prenons le premier prénom, regardons le nombre de bigrammes qu’il contient :

chs = ['.'] + list(words[0]) + ['.']
for ch1, ch2 in zip(chs, chs[1:]):
  bigram = (ch1, ch2)
  print(bigram)

('.', 'M')
('M', 'A')
('A', 'R')
('R', 'I')
('I', 'E')
('E', '.')

Le prénom “Marie” contient 6 bigrammes.

Méthode par comptage

Construisons maintenant un dictionnaire Python qui regroupe tous les bigrammes du dataset en comptant leurs occurrences.

b = {}
for w in words:
  chs = ['.'] + list(w) + ['.']
  for ch1, ch2 in zip(chs, chs[1:]):
    bigram = (ch1, ch2)
    b[bigram] = b.get(bigram, 0) + 1
sorted(b.items(), key = lambda kv: -kv[1])
print('Les 5 bigrammes les plus fréquents : ',sorted(b.items(), key = lambda kv: -kv[1])[:5])

Les 5 bigrammes les plus fréquents :  [(('A', '.'), 7537), (('E', '.'), 6840), (('A', 'N'), 6292), (('N', '.'), 3741), (('N', 'E'), 3741)]

On a donc notre dictionnaire de fréquence des bigrammes dans l’intégralité du dataset. Comme on peut le voir, il est fréquent que des prénoms se terminent par A, E ou N, et que les lettres A et N se suivent, ainsi que les lettres N et E.

Matrice d’occurrences

Il est plus simple de visualiser et de traiter les données sous forme matricielle. On va construire une matrice de taille 46x46 (45 caractères + le caractère spécial ‘.’) où la ligne correspond à la première lettre et la colonne à la seconde.

import torch
N = torch.zeros((46, 46), dtype=torch.int32)

On va trier nos caractères et créer des tables de recherche (look-up tables) avec l’objet dictionnaire de Python. On veut pouvoir passer d’un caractère à un entier (pour indexer dans la matrice) et inversement (pour reconstruire les prénoms à partir d’entiers).

chars = sorted(list(set(''.join(words))))
stoi = {s:i+1 for i,s in enumerate(chars)}
stoi['.'] = 0
itos = {i:s for s,i in stoi.items()}

On va maintenant remplir notre matrice :

for w in words:
  chs = ['.'] + list(w) + ['.']
  for ch1, ch2 in zip(chs, chs[1:]):
    ix1 = stoi[ch1]
    ix2 = stoi[ch2]
    N[ix1, ix2] += 1

Et on peut maintenant afficher la matrice (look-up table).

#Code pour dessiner une jolie matrice
import matplotlib.pyplot as plt
%matplotlib inline

plt.figure(figsize=(32,32))
plt.imshow(N, cmap='Blues')
for i in range(46):
  for j in range(46):
    chstr = itos[i] + itos[j]
    plt.text(j, i, chstr, ha="center", va="bottom", color='gray')
    plt.text(j, i, N[i, j].item(), ha="center", va="top", color='gray')
plt.axis('off');

Probabilités

Pour connaître la probabilité qu’un prénom commence par une certaine lettre, il faut regarder la ligne du caractère ‘.’, c’est-à-dire la ligne 0, et normaliser chaque valeur par la somme des valeurs de cette ligne (pour obtenir des valeurs entre 0 et 1 dont la somme est égale à 1).

p = N[0].float()
p = p / p.sum()
print("Compte de la première ligne : ",N[0])
print("Probabilités : ",p)

Compte de la première ligne :  tensor([   0,    0,    0, 3399,  825, 1483, 1208, 1400,  864,  907, 1039,  788,
        1352, 1503, 2108, 3606, 1501,  546,  620,   32, 1142, 2539, 1185,   72,
         329,  294,   29,  661,  393,    0,    2,    0,    0,    1,    2,  161,
           0,    0,    2,    2,    0,    5,    0,    0,    0,    0],
       dtype=torch.int32)
Probabilités :  tensor([0.0000e+00, 0.0000e+00, 0.0000e+00, 1.1330e-01, 2.7500e-02, 4.9433e-02,
        4.0267e-02, 4.6667e-02, 2.8800e-02, 3.0233e-02, 3.4633e-02, 2.6267e-02,
        4.5067e-02, 5.0100e-02, 7.0267e-02, 1.2020e-01, 5.0033e-02, 1.8200e-02,
        2.0667e-02, 1.0667e-03, 3.8067e-02, 8.4633e-02, 3.9500e-02, 2.4000e-03,
        1.0967e-02, 9.8000e-03, 9.6667e-04, 2.2033e-02, 1.3100e-02, 0.0000e+00,
        6.6667e-05, 0.0000e+00, 0.0000e+00, 3.3333e-05, 6.6667e-05, 5.3667e-03,
        0.0000e+00, 0.0000e+00, 6.6667e-05, 6.6667e-05, 0.0000e+00, 1.6667e-04,
        0.0000e+00, 0.0000e+00, 0.0000e+00, 0.0000e+00])

Pour générer des prénoms de manière aléatoire, on ne veut pas toujours choisir la lettre la plus probable (car on générerait toujours le même prénom). On veut choisir une lettre en fonction de sa probabilité. Si la lettre ‘n’ a une probabilité de 0,1, on veut la choisir 10% du temps. Pour cela, on utilise la fonction torch.multinomial de PyTorch.

ix = torch.multinomial(p, num_samples=1, replacement=True).item()
itos[ix]

'Z'

À chaque appel, on obtient une lettre différente en fonction de sa probabilité d’apparition dans notre dataset de test.

Avec tous ces éléments, on est maintenant prêt à générer des prénoms à partir de notre matrice N. L’idéal serait de créer une matrice avec directement les probabilités pour éviter de renormaliser à chaque fois.

# On copie N et on la convertit en float
P = N.float()
# On normalise chaque ligne
# On somme sur la première dimension (les colonnes)
print("Somme des lignes : ",P.sum(1, keepdims=True).shape)
P /= P.sum(1, keepdims=True) # /= est un raccourci pour P = P / P.sum(1, keepdims=True)
print("Matrice normalisée P est de taille : ",P.shape)
# On vérifie que la somme d'une ligne est égale à 1
print("Somme de la première ligne de P : ",P.sum(1)[0].item())

Somme des lignes :  torch.Size([46, 1])
Matrice normalisée P est de taille :  torch.Size([46, 46])
Somme de la première ligne de P :  1.0

Point sur la division de matrices de tailles différentes : Comme vous l’avez remarqué, on divise une matrice de taille (46,46) par une matrice de taille (46,1), ce qui semble impossible. Avec PyTorch, il existe des règles de broadcasting. Je vous recommande vivement de vous familiariser avec ce concept, car c’est une source d’erreurs fréquente. Pour comprendre en détail les règles de broadcasting, vous pouvez consulter le cours bonus. En pratique, diviser une matrice de taille (46,46) par une matrice de taille (46,1) va “broadcaster” la matrice (46,1) en (46,46) en copiant 46 fois la matrice de base. Cela permet de réaliser l’opération comme souhaité.

Génération

Il est enfin temps de générer des prénoms avec notre méthode bigramme ! Nous allons définir une fonction pour générer des prénoms :

def genName():
  out = []
  ix = 0 # On commence par '.'
  while True: # Tant qu'on n'a pas généré le caractère '.'
    p = P[ix] # On récupère la distribution de probabilité de la ligne correspondant au caractère actuel
    ix = torch.multinomial(p, num_samples=1, replacement=True).item() # On tire un échantillon
    out.append(itos[ix]) # On ajoute le caractère à notre prénom
    if ix == 0:
      break
  return ''.join(out)
genName()

'MARAUSUR.'

On peut par exemple générer 10 prénoms aléatoires :

for i in range(10):
  print(genName())

DA.
TYEYSE-SSCL.
DE.
ANINEDANDVI.
SOKE.
RENNA.
FUXA.
EROA.
FA.
KALEN.

Comme vous pouvez le constater, la génération est assez mauvaise… Pourquoi ? Parce que le bigramme est une méthode très limitée. Se baser uniquement sur le dernier caractère ne permet pas d’avoir une connaissance suffisante pour générer des prénoms corrects.

Évaluation du modèle

Maximum de vraisemblance ou likelihood

On veut maintenant évaluer notre modèle sur l’ensemble d’entraînement. Pour cela, on utilise le maximum de vraisemblance, comme dans le second notebook du cours 1. Le maximum de vraisemblance ou likelihood est une mesure correspondant au produit des probabilités des événements. Pour avoir un bon modèle, on cherche à maximiser le likelihood.

productOfProbs = 1
for w in words[:2]:
  chs = ['.'] + list(w) + ['.']
  for ch1, ch2 in zip(chs, chs[1:]):
    ix1 = stoi[ch1]
    ix2 = stoi[ch2]
    prob = P[ix1, ix2]
    productOfProbs *= prob
    print(f"La probabilité de {ch1}->{ch2} est {prob.item():.3f}")
print("Le produit des probabilités est : ",productOfProbs.item())

La probabilité de .->M est 0.120
La probabilité de M->A est 0.431
La probabilité de A->R est 0.084
La probabilité de R->I est 0.256
La probabilité de I->E est 0.119
La probabilité de E->. est 0.321
La probabilité de .->J est 0.045
La probabilité de J->E est 0.232
La probabilité de E->A est 0.024
La probabilité de A->N est 0.201
La probabilité de N->. est 0.212
Le produit des probabilités est :  4.520583629652464e-10

On voit rapidement que multiplier les probabilités pose problème. Ici, on les multiplie sur 2 des 30 000 éléments du dataset et on obtient une valeur très faible. Si on les multiplie sur l’ensemble du dataset, on obtient une valeur non représentable par un ordinateur.

Log-likelihood

Pour résoudre ce problème de précision, on utilise le logarithme pour plusieurs raisons :

• La fonction log est monotone, c’est-à-dire que si \(a > b\), alors \(log(a) > log(b)\). Maximiser le log-likelihood est équivalent à maximiser le likelihood dans un contexte d’optimisation.

• Une propriété intéressante des logarithmes (qui explique pourquoi cette fonction est souvent utilisée en optimisation et en probabilité) est la règle suivante : \(log(a \times b) = log(a) + log(b)\). Cela nous permet d’éviter de multiplier de petites valeurs qui pourraient dépasser la précision d’un ordinateur.

On peut donc maximiser le log-likelihood plutôt que le likelihood. Reprenons la boucle précédente et regardons ce que cela donne :

sumOfLogs = 0
for w in words[:2]:
  chs = ['.'] + list(w) + ['.']
  for ch1, ch2 in zip(chs, chs[1:]):
    ix1 = stoi[ch1]
    ix2 = stoi[ch2]
    prob = P[ix1, ix2]
    sumOfLogs += torch.log(prob)
print("La somme des log est : ",sumOfLogs.item())

La somme des log est :  -21.517210006713867

On obtient une valeur beaucoup plus raisonnable. Pour les problèmes d’optimisation, on préfère souvent avoir une fonction à minimiser. Dans le cas d’un modèle parfait, chaque probabilité vaut 1, donc chaque log vaut 0, et la somme des logs vaut 0. Sinon, on obtient des valeurs négatives, car une probabilité est toujours inférieure à 1 et \(log(a) < 0 \text{ si } a < 1\). Pour avoir un problème de minimisation, on utilise le negative log-likelihood, qui correspond simplement à l’opposé du log-likelihood.

Souvent, on prend la moyenne plutôt que la somme, car c’est plus lisible et équivalent en termes d’optimisation. Et nous allons le calculer sur l’ensemble des prénoms du dataset.

sumOfLogs = 0
n=0
for w in words:
  chs = ['.'] + list(w) + ['.']
  for ch1, ch2 in zip(chs, chs[1:]):
    ix1 = stoi[ch1]
    ix2 = stoi[ch2]
    prob = P[ix1, ix2]
    sumOfLogs += - torch.log(prob)
    n+=1
print("La somme des negative log est : ",sumOfLogs.item())
print("La moyenne des negative log est : ",sumOfLogs.item()/n)

La somme des negative log est :  564925.125
La moyenne des negative log est :  2.4960792002651053

Le negative log-likelihood du dataset est donc de 2,49.

Vous pouvez également voir si votre prénom est commun ou peu commun par rapport à la moyenne du dataset. Pour cela, il suffit de remplacer mon prénom “SIMON” par le vôtre (en majuscules).

sumOfLogs = 0
n=0
for w in "SIMON":
  chs = ['.'] + list(w) + ['.']
  for ch1, ch2 in zip(chs, chs[1:]):
    ix1 = stoi[ch1]
    ix2 = stoi[ch2]
    prob = P[ix1, ix2]
    sumOfLogs += - torch.log(prob)
    n+=1
print("La moyenne des negative log est : ",sumOfLogs.item()/n)

La moyenne des negative log est :  2.598056602478027

Si la valeur du negative log-likelihood correspondant à votre prénom est inférieure à celle du dataset, votre prénom est assez commun. Sinon, il est plutôt peu commun.

Approche par réseau de neurones

Problème de l’approche “comptage”

Nous allons maintenant essayer de résoudre le même problème d’une manière différente. Nous avons résolu ce problème en comptant simplement les occurrences des bigrammes et en calculant la probabilité par rapport à cela. Cette méthode fonctionne pour des bigrammes, mais ne fonctionnera pas pour des choses plus complexes comme des N-grammes.

En effet, notre table de recherche est de taille 46x46 pour deux caractères. Si on considère N caractères (donc N-1 caractères pour prédire le N-ième), on a tout de suite beaucoup plus de possibilités. On peut calculer simplement que la table sera de taille \(46^N\). Pour N=4, cela donnerait une table de taille 4 477 456. Autant dire que pour des valeurs de contexte importantes (les modèles d’aujourd’hui ont un contexte de dizaines de milliers de tokens et il y a plus de 46 possibilités à chaque fois), cette approche ne fonctionnera pas du tout.

C’est pourquoi l’approche par réseau de neurones est très intéressante. Dans la suite du cours, nous allons montrer comment résoudre ce même problème à l’aide d’un réseau de neurones, ce qui vous donnera une intuition sur les capacités du réseau lorsque le contexte augmente.

Dataset de notre réseau de neurones

Notre réseau de neurones va recevoir un caractère en entrée et devra prédire le caractère suivant. Comme fonction de perte, on pourra utiliser la fonction negative log-likelihood pour essayer de se rapprocher de la valeur du bigramme par “comptage”.

Commençons par créer notre dataset d’entraînement. On reprend la boucle de parcours des bigrammes de la partie précédente et cette fois, on indexe deux listes : xs pour les entrées et ys pour les labels.

# create the training set of bigrams (x,y)
xs, ys = [], []

for w in words[:1]:
  chs = ['.'] + list(w) + ['.']
  for ch1, ch2 in zip(chs, chs[1:]):
    ix1 = stoi[ch1]
    ix2 = stoi[ch2]
    print(ch1, ch2)
    xs.append(ix1)
    ys.append(ix2)
    
xs = torch.tensor(xs)
ys = torch.tensor(ys)

. M
M A
A R
R I
I E
E .

print("valeurs d'entrée : ",xs)
print("valeurs de sortie : ",ys)

valeurs d'entrée :  tensor([ 0, 15,  3, 20, 11,  7])
valeurs de sortie :  tensor([15,  3, 20, 11,  7,  0])

Pour la valeur d’entrée 0, qui correspond à ‘.’, on veut prédire un label 15, qui correspond à ‘M’.

Le problème de ces listes, c’est qu’elles contiennent des entiers, et il n’est pas possible de donner un entier en entrée d’un réseau de neurones. Dans le domaine du NLP, on utilise souvent le one-hot encoding, qui consiste à convertir un index en un vecteur de 0 avec un 1 à la position de l’index. La taille du vecteur correspond au nombre de classes possibles, donc ici 46.

import torch.nn.functional as F
# one-hot encoding
xenc = F.one_hot(xs, num_classes=46).float() # conversion en float pour le NN
print("Encodage one-hot des deux premiers caractères: ",xenc[:2])

Encodage one-hot des deux premiers caractères:  tensor([[1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])

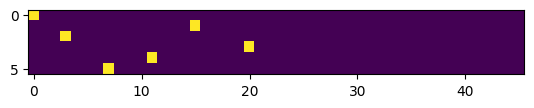
Comme vous pouvez le voir, on a un 1 à la position 0 du premier vecteur et un 1 à la position 15 du second. Ce sont ces vecteurs qui serviront d’entrée à notre réseau de neurones. On peut visualiser à quoi ressemblent ces vecteurs pour avoir une meilleure intuition de ce que fait le one-hot encoding.

# Les 5 premiers vecteurs one-hot
plt.imshow(xenc)

<matplotlib.image.AxesImage at 0x784579d81f10>

Notre réseau de neurones

Nous allons maintenant créer notre réseau de neurones. Il s’agira d’un réseau de neurones extrêmement simple contenant une seule couche. Pour la taille de la couche, nous prenons en entrée un vecteur de taille \(n \times 46\), il faudra donc une première dimension de taille 46. En sortie, on veut une distribution de probabilité sur l’ensemble des caractères. Notre couche de réseau sera donc de taille \(46 \times 46\).

Commençons par initialiser notre couche avec des valeurs aléatoires :

# On met le paramètre requires_grad à True pour pouvoir optimiser la matrice par descente de gradient
W = torch.randn((46, 46), requires_grad=True) 

Le forward de notre réseau de neurones consistera simplement en une multiplication matricielle entre l’entrée et la couche. On appliquera ensuite la fonction softmax (voir cours sur les CNN) pour obtenir une distribution de probabilités.

# One hot encoding sur les entrées
xenc = F.one_hot(xs, num_classes=46).float() 
# Multiplication matricielle (forward pass)
logits = xenc @ W  # @ est la multiplication matricielle
#Softmax pour obtenir des probabilités
counts = logits.exp() 
probs = counts / counts.sum(1, keepdims=True) 
print(probs.shape)

torch.Size([6, 46])

On obtient une distribution de probabilités pour chacun de nos 6 caractères. On va visualiser les sorties de notre réseau de neurones non entraîné et calculer le negative log-likelihood pour voir où l’on se situe par rapport à notre modèle obtenu par “comptage”.

nlls = torch.zeros(6)
for i in range(6):
  x = xs[i].item() # index de l'entrée
  y = ys[i].item() # index du label
  print('--------')
  print(f'bigramme actuel {i+1}: {itos[x]}{itos[y]} (indexes {x},{y})')
  print('entrée du réseau de neurones :', x)
  print('sortie du réseau (probabilité) :', probs[i])
  print('vrai label :', y)
  p = probs[i, y]
  print('probabilité donné par le réseau sur le caractère réel :', p.item())
  logp = torch.log(p)
  nll = -logp
  print('negative log likelihood:', nll.item())
  nlls[i] = nll

print('=========')
print('negative log likelihood moyen, i.e. loss =', nlls.mean().item())

--------
bigramme actuel 1: .M (indexes 0,15)
entrée du réseau de neurones : 0
sortie du réseau (probabilité) : tensor([0.0146, 0.0210, 0.0823, 0.0077, 0.0160, 0.0483, 0.0943, 0.0204, 0.0079,
        0.0112, 0.0085, 0.0179, 0.0188, 0.0292, 0.0022, 0.0092, 0.0200, 0.0094,
        0.0097, 0.0191, 0.1091, 0.0122, 0.0092, 0.0287, 0.0120, 0.0088, 0.0053,
        0.0217, 0.0177, 0.0050, 0.0038, 0.0483, 0.0320, 0.0441, 0.0105, 0.0126,
        0.0266, 0.0092, 0.0262, 0.0081, 0.0430, 0.0012, 0.0102, 0.0025, 0.0126,
        0.0116], grad_fn=<SelectBackward0>)
vrai label : 15
probabilité donné par le réseau sur le caractère réel : 0.009214116260409355
negative log likelihood: 4.687018394470215
--------
bigramme actuel 2: MA (indexes 15,3)
entrée du réseau de neurones : 15
sortie du réseau (probabilité) : tensor([0.0574, 0.1353, 0.0227, 0.0032, 0.1142, 0.0148, 0.1007, 0.0162, 0.0242,
        0.0089, 0.0040, 0.0459, 0.0023, 0.0081, 0.0064, 0.0124, 0.0083, 0.0112,
        0.0172, 0.0062, 0.0033, 0.0045, 0.0131, 0.0144, 0.0218, 0.0080, 0.0225,
        0.0097, 0.0164, 0.0074, 0.0165, 0.0091, 0.0412, 0.0087, 0.0100, 0.0039,
        0.0080, 0.0036, 0.0377, 0.0150, 0.0345, 0.0048, 0.0253, 0.0036, 0.0164,
        0.0210], grad_fn=<SelectBackward0>)
vrai label : 3
probabilité donné par le réseau sur le caractère réel : 0.0031920599285513163
negative log likelihood: 5.74708890914917
--------
bigramme actuel 3: AR (indexes 3,20)
entrée du réseau de neurones : 3
sortie du réseau (probabilité) : tensor([0.0199, 0.0169, 0.0239, 0.0122, 0.0174, 0.0203, 0.0043, 0.0822, 0.0517,
        0.0228, 0.0118, 0.0121, 0.0210, 0.0088, 0.0063, 0.0128, 0.1041, 0.0100,
        0.0338, 0.0772, 0.0056, 0.0565, 0.0134, 0.0032, 0.0253, 0.0120, 0.0337,
        0.0080, 0.0083, 0.0060, 0.0068, 0.0020, 0.0405, 0.0120, 0.0366, 0.0080,
        0.0111, 0.0135, 0.0164, 0.0038, 0.0133, 0.0029, 0.0094, 0.0047, 0.0504,
        0.0271], grad_fn=<SelectBackward0>)
vrai label : 20
probabilité donné par le réseau sur le caractère réel : 0.005596297327429056
negative log likelihood: 5.185649871826172
--------
bigramme actuel 4: RI (indexes 20,11)
entrée du réseau de neurones : 20
sortie du réseau (probabilité) : tensor([0.0030, 0.0300, 0.0056, 0.0311, 0.0361, 0.0294, 0.0462, 0.0163, 0.0369,
        0.0178, 0.0251, 0.0125, 0.0162, 0.0019, 0.0828, 0.0173, 0.0068, 0.0113,
        0.0204, 0.0124, 0.0653, 0.0059, 0.0038, 0.0075, 0.0165, 0.0332, 0.0065,
        0.0354, 0.0169, 0.0062, 0.0683, 0.0203, 0.0189, 0.0179, 0.0113, 0.0119,
        0.0549, 0.0035, 0.0051, 0.0061, 0.0569, 0.0268, 0.0164, 0.0021, 0.0146,
        0.0088], grad_fn=<SelectBackward0>)
vrai label : 11
probabilité donné par le réseau sur le caractère réel : 0.012452212162315845
negative log likelihood: 4.385857105255127
--------
bigramme actuel 5: IE (indexes 11,7)
entrée du réseau de neurones : 11
sortie du réseau (probabilité) : tensor([0.0265, 0.0211, 0.0312, 0.0235, 0.0020, 0.0151, 0.0145, 0.0083, 0.0141,
        0.0062, 0.0168, 0.0183, 0.0600, 0.0047, 0.0969, 0.0438, 0.0083, 0.0584,
        0.0572, 0.0061, 0.0159, 0.0475, 0.0079, 0.0116, 0.0331, 0.0043, 0.0049,
        0.0134, 0.0057, 0.0077, 0.0350, 0.0276, 0.0174, 0.0050, 0.0176, 0.0022,
        0.0169, 0.0029, 0.0281, 0.0115, 0.0291, 0.0250, 0.0071, 0.0126, 0.0277,
        0.0491], grad_fn=<SelectBackward0>)
vrai label : 7
probabilité donné par le réseau sur le caractère réel : 0.008320074528455734
negative log likelihood: 4.789083957672119
--------
bigramme actuel 6: E. (indexes 7,0)
entrée du réseau de neurones : 7
sortie du réseau (probabilité) : tensor([0.0397, 0.0266, 0.0185, 0.0024, 0.0054, 0.0061, 0.0143, 0.0269, 0.0398,
        0.0084, 0.0134, 0.0247, 0.1220, 0.0039, 0.0062, 0.0829, 0.0452, 0.0086,
        0.0062, 0.0130, 0.0106, 0.0137, 0.0073, 0.1132, 0.0146, 0.0252, 0.0112,
        0.0955, 0.0133, 0.0196, 0.0091, 0.0122, 0.0160, 0.0092, 0.0128, 0.0337,
        0.0058, 0.0112, 0.0070, 0.0029, 0.0033, 0.0073, 0.0052, 0.0049, 0.0125,
        0.0087], grad_fn=<SelectBackward0>)
vrai label : 0
probabilité donné par le réseau sur le caractère réel : 0.0397193469107151
negative log likelihood: 3.225916862487793
=========
negative log likelihood moyen, i.e. loss = 4.670102596282959

Pour le calcul de la perte, on va calculer le negative log-likelihood de la sortie de notre réseau par rapport au label de la manière suivante :

# Calcul de la loss
loss = -probs[torch.arange(6), ys].log().mean()
print(loss.item())
# On remet les gradients à zéro (None est plus efficace)
W.grad = None 
# Calcul des gradients automatique de pytorch
loss.backward()
print(W.grad)

4.670102596282959
tensor([[0.0024, 0.0035, 0.0137,  ..., 0.0004, 0.0021, 0.0019],
        [0.0000, 0.0000, 0.0000,  ..., 0.0000, 0.0000, 0.0000],
        [0.0000, 0.0000, 0.0000,  ..., 0.0000, 0.0000, 0.0000],
        ...,
        [0.0000, 0.0000, 0.0000,  ..., 0.0000, 0.0000, 0.0000],
        [0.0000, 0.0000, 0.0000,  ..., 0.0000, 0.0000, 0.0000],
        [0.0000, 0.0000, 0.0000,  ..., 0.0000, 0.0000, 0.0000]])

Comme vous pouvez le voir, on a calculé les gradients de notre matrice W par rapport au loss. De la même manière que dans les cours précédents, on peut mettre à jour les poids du modèle dans le sens du gradient avec un pas (le learning_rate).

# avec un learning_rate de 0.1
W.data += -0.1 * W.grad

Optimisation

À partir de tout ce que nous venons de voir, nous pouvons maintenant rassembler les éléments et optimiser notre modèle.

Création du dataset complet On va commencer par créer notre dataset complet en reprenant la boucle précédente, mais en parcourant l’ensemble des prénoms.

xs, ys = [], []
for w in words:
  chs = ['.'] + list(w) + ['.']
  for ch1, ch2 in zip(chs, chs[1:]):
    ix1 = stoi[ch1]
    ix2 = stoi[ch2]
    xs.append(ix1)
    ys.append(ix2)
xs = torch.tensor(xs)
ys = torch.tensor(ys)
num = xs.nelement()
print('number of examples: ', num)

number of examples:  226325

Initialisation du modèle On peut maintenant initialiser notre modèle comme précédemment, choisir le learning_rate et le nombre d’itérations.

W = torch.randn((46, 46), requires_grad=True)
lr=50 # en pratique, dans ce petit problème, un learning rate de 50 fonctionne bien ce qui peut sembler étonnant
iterations=100

Descente du gradient Appliquons maintenant l’algorithme de descente du gradient sur notre modèle.

# Descente du gradient
for k in range(iterations):
  
  # forward pass
  xenc = F.one_hot(xs, num_classes=46).float() # transformation one hot sur les entrées
  logits = xenc @ W
  probs=F.softmax(logits,dim=1) # On applique le softmax
  loss = -probs[torch.arange(num), ys].log().mean() # Calcul du negative log likelihood (loss)
  if k%10==0:
    print('loss iteration '+str(k)+' : ',loss.item())
  
  # retropropagation
  W.grad = None # Remettre la gradient à zéro à chaque itération (à ne pas oublier !!!!)
  loss.backward()
  
  # Mise à jour des poids
  W.data += -50 * W.grad

loss iteration 0 :  4.346113204956055
loss iteration 10 :  2.94492769241333
loss iteration 20 :  2.7590363025665283
loss iteration 30 :  2.6798315048217773
loss iteration 40 :  2.637108087539673
loss iteration 50 :  2.610524892807007
loss iteration 60 :  2.5923469066619873
loss iteration 70 :  2.5791807174682617
loss iteration 80 :  2.569261074066162
loss iteration 90 :  2.561541795730591

Après 100 itérations, on obtient un negative log-likelihood proche de celui du modèle par “comptage”. C’est en fait la capacité maximale du modèle bigramme sur les données d’entraînement.

Génération de prénoms avec notre modèle On peut maintenant générer des prénoms avec notre modèle.

for i in range(5):
  
  out = []
  ix = 0
  while True:
    xenc = F.one_hot(torch.tensor([ix]), num_classes=46).float()
    logits = xenc @ W 
    # Prédiction des probabilités de la lettre suivante
    p=F.softmax(logits,dim=1)
    
    # On fait un tirage aléatoire de la prochaine lettre en suivante la distribution p 
    ix = torch.multinomial(p, num_samples=1, replacement=True).item()
    # Conversion en lettre
    out.append(itos[ix])
    if ix == 0:
      break
  print(''.join(out))

JE.
S.
ADJULA.
M.
LVERTYÜCI.

Notes supplémentaires

La matrice de poids \(W\) a la même taille que la matrice \(N\) utilisée dans la méthode par comptage. Ce que nous venons de réaliser avec l’approche par réseau de neurones est en fait l’apprentissage de la matrice \(N\). On peut confirmer cette intuition en regardant ce qu’il se passe lorsqu’on fait l’opération xenc @ W. Il s’agit d’une multiplication matricielle d’une matrice ligne de taille \(1 \times 46\) par une matrice carrée de taille \(46 \times 46\). De plus, la matrice ligne contient uniquement des zéros, sauf un 1 à l’index \(i\) de la lettre. Cette multiplication matricielle donne en résultat la ligne \(i\) de la matrice \(W\). Cela correspond exactement à ce qu’on faisait dans la méthode par comptage, où l’on récupérait les probabilités de la ligne \(i\) de \(P\).