Normalización por lotes (Batch Normalization)

La Normalización por Lotes (Batch Normalization) fue introducida en 2015 en el artículo Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. Tuvo un impacto significativo en el campo del Deep Learning. Actualmente, la normalización se utiliza casi sistemáticamente, ya sea BatchNorm, LayerNorm o GroupNorm (entre otras).

La idea detrás de BatchNorm es simple y está relacionada con el cuaderno anterior. Buscamos obtener preactivaciones que sigan una distribución gaussiana en cada capa de la red. Hemos visto que una buena inicialización permite lograr este comportamiento, pero no siempre es evidente, especialmente con muchas capas diferentes.

BatchNorm normaliza las preactivaciones con respecto a la dimensión del batch antes de pasarlas por las funciones de activación. Esto garantiza una distribución gaussiana en cada paso.

Esta normalización no afecta la optimización, ya que se trata de una función derivable.

Implementación

Reutilización del código

Vamos a reutilizar el código del cuaderno anterior para implementar la normalización por lotes.

import torch
import torch.nn.functional as F
%matplotlib inline

words = open('../05_NLP/prenoms.txt', 'r').read().splitlines()
chars = sorted(list(set(''.join(words))))
stoi = {s:i+1 for i,s in enumerate(chars)}
stoi['.'] = 0
itos = {i:s for s,i in stoi.items()}

block_size = 3 # Contexte

def build_dataset(words):  
  X, Y = [], []
  
  for w in words:
    context = [0] * block_size
    for ch in w + '.':
      ix = stoi[ch]
      X.append(context)
      Y.append(ix)
      context = context[1:] + [ix] 

  X = torch.tensor(X)
  Y = torch.tensor(Y)
  print(X.shape, Y.shape)
  return X, Y

import random
random.seed(42)
random.shuffle(words)
n1 = int(0.8*len(words))
n2 = int(0.9*len(words))

Xtr,  Ytr  = build_dataset(words[:n1])     # 80%
Xdev, Ydev = build_dataset(words[n1:n2])   # 10%
Xte,  Yte  = build_dataset(words[n2:])     # 10%

torch.Size([180834, 3]) torch.Size([180834])
torch.Size([22852, 3]) torch.Size([22852])
torch.Size([22639, 3]) torch.Size([22639])

embed_dim=10 # Dimension de l'embedding de C
hidden_dim=200 # Dimension de la couche cachée

C = torch.randn((46, embed_dim))
W1 = torch.randn((block_size*embed_dim, hidden_dim))*0.01 # On initialise les poids à une petite valeur
b1 = torch.randn(hidden_dim) *0 # On initialise les biais à 0
W2 = torch.randn((hidden_dim, 46))*0.01
b2 = torch.randn(46)*0 
parameters = [C, W1, b1, W2, b2]
for p in parameters:
  p.requires_grad = True

Este es nuestro código de propagación hacia adelante:

batch_size = 32

ix = torch.randint(0, Xtr.shape[0], (batch_size,))
  
# Forward
Xb, Yb = Xtr[ix], Ytr[ix] 
emb = C[Xb] 
embcat = emb.view(emb.shape[0], -1)
hpreact = embcat @ W1 + b1 

h = torch.tanh(hpreact) 
logits = h @ W2 + b2 
loss = F.cross_entropy(logits, Yb)

Implementación de BatchNorm

Según el artículo, esta es la información:

En primer lugar, se trata de normalizar.

Para ello, calculamos la media y la desviación estándar de hpreact y luego normalizamos con estos valores:

epsilon=1e-6
hpreact_mean = hpreact.mean(dim=0, keepdim=True)
hpreact_std= hpreact.std(dim=0, keepdim=True)
hpreact_norm = (hpreact - hpreact_mean) / (hpreact_std+epsilon)

Ahora podemos integrar esta normalización en la propagación hacia adelante.

Antes de eso, observemos que aún no hemos implementado la parte de escala y desplazamiento (scale and shift):

¿Para qué sirve? La normalización confina los pesos a tomar valores de una gaussiana centrada y reducida. Esto limita la capacidad de expresión del modelo. Los parámetros aprendibles \(\gamma\) y \(\beta\) permiten evitar este problema al añadir un desplazamiento con \(\beta\) y una escala con \(\gamma\).

Dado que se trata de parámetros aprendibles, también debemos agregarlos a los parámetros del modelo:

C = torch.randn((46, embed_dim))
W1 = torch.randn((block_size*embed_dim, hidden_dim))*0.01 # On initialise les poids à une petite valeur
b1 = torch.randn(hidden_dim) *0 # On initialise les biais à 0
W2 = torch.randn((hidden_dim, 46))*0.01
b2 = torch.randn(46)*0 
# Paramètres de batch normalization
bngain = torch.ones((1, hidden_dim))
bnbias = torch.zeros((1, hidden_dim))

parameters = [C, W1, b1, W2, b2, bngain, bnbias]
for p in parameters:
  p.requires_grad = True

Por lo tanto, en la propagación hacia adelante tendremos:

batch_size = 32

ix = torch.randint(0, Xtr.shape[0], (batch_size,))
  
# Forward
Xb, Yb = Xtr[ix], Ytr[ix] 
emb = C[Xb] 
embcat = emb.view(emb.shape[0], -1)
hpreact = embcat @ W1 + b1 

# Batch normalization
bnmean = hpreact.mean(0, keepdim=True)
bnstd = hpreact.std(0, keepdim=True)
hpreact = bngain * (hpreact - bnmean) / bnstd + bnbias

h = torch.tanh(hpreact) 
logits = h @ W2 + b2 
loss = F.cross_entropy(logits, Yb)

El problema de la Normalización por Lotes

Al reflexionar un poco, podemos identificar problemas potenciales relacionados con BatchNorm:

Un ejemplo se ve afectado por otros elementos del batch: Normalizar según la dimensión del batch significa que los valores de cada ejemplo dentro del batch están influenciados por los otros ejemplos. Esto podría parecer problemático, pero en la práctica es algo positivo. El uso de batches aleatorios en cada época permite una regularización, lo que reduce el riesgo de sobreajuste (overfit) en los datos. Sin embargo, si queremos evitar este problema, podemos utilizar otros métodos de normalización que no normalicen según la dimensión del batch. En la práctica, la BatchNorm sigue siendo ampliamente utilizada porque funciona muy bien empíricamente.

Fase de prueba en un solo elemento: Durante el entrenamiento, cada elemento está influenciado por los otros elementos de su batch. Sin embargo, en la fase de inferencia, cuando usamos el modelo en un solo elemento, ya no podemos aplicar BatchNorm. Esto es un problema, ya que queremos evitar un comportamiento diferente durante el entrenamiento y la inferencia.

Para resolver este problema, tenemos dos soluciones:

• Podemos calcular la media y la varianza sobre el conjunto de elementos al final del entrenamiento y usar estos valores. En la práctica, no queremos hacer una iteración adicional sobre todo el conjunto de datos solo para esto, por lo que nadie lo hace así.

• Otra solución consiste en actualizar la media y la varianza a lo largo del entrenamiento mediante un EMA (promedio móvil exponencial). Al final del entrenamiento, tendremos una buena aproximación de la media y la varianza de todos los elementos de entrenamiento.

En la práctica, podemos implementarlo en Python de la siguiente manera:

C = torch.randn((46, embed_dim))
W1 = torch.randn((block_size*embed_dim, hidden_dim))*0.01 # On initialise les poids à une petite valeur
b1 = torch.randn(hidden_dim) *0 # On initialise les biais à 0
W2 = torch.randn((hidden_dim, 46))*0.01
b2 = torch.randn(46)*0 
# Paramètres de batch normalization
bngain = torch.ones((1, hidden_dim))
bnbias = torch.zeros((1, hidden_dim))
bnmean_running = torch.zeros((1, hidden_dim))
bnstd_running = torch.ones((1, hidden_dim))

parameters = [C, W1, b1, W2, b2, bngain, bnbias]
for p in parameters:
  p.requires_grad = True

batch_size = 32

ix = torch.randint(0, Xtr.shape[0], (batch_size,))
  
# Forward
Xb, Yb = Xtr[ix], Ytr[ix] 
emb = C[Xb] 
embcat = emb.view(emb.shape[0], -1)
hpreact = embcat @ W1 + b1 

# Batch normalization
bnmeani = hpreact.mean(0, keepdim=True)
bnstdi = hpreact.std(0, keepdim=True)
hpreact = bngain * (hpreact - bnmeani) / bnstdi + bnbias
with torch.no_grad(): # On ne veut pas calculer de gradient pour ces opérations
    bnmean_running = 0.999 * bnmean_running + 0.001 * bnmeani
    bnstd_running = 0.999 * bnstd_running + 0.001 * bnstdi

h = torch.tanh(hpreact) 
logits = h @ W2 + b2 
loss = F.cross_entropy(logits, Yb)

Nota: En nuestra implementación, hemos elegido 0.001 para nuestro EMA. En la capa BatchNorm de PyTorch, este parámetro está definido por momentum y su valor predeterminado es 0.1. En la práctica, la elección de este valor depende del tamaño del batch en relación con el tamaño del conjunto de datos de entrenamiento. Por ejemplo, para un batch grande con un conjunto de datos pequeño, podemos tomar 0.1. Para un batch pequeño con un conjunto de datos grande, es mejor elegir un valor más pequeño.

Probemos ahora el entrenamiento de nuestro modelo para verificar que la capa funcione. Para este pequeño modelo, no habrá diferencia en el rendimiento.

lossi = []
max_steps = 200000

for i in range(max_steps):
  ix = torch.randint(0, Xtr.shape[0], (batch_size,))
  Xb, Yb = Xtr[ix], Ytr[ix] 
  emb = C[Xb] 
  embcat = emb.view(emb.shape[0], -1)
  hpreact = embcat @ W1 + b1 
  
  # Batch normalization
  bnmeani = hpreact.mean(0, keepdim=True)
  bnstdi = hpreact.std(0, keepdim=True)
  hpreact = bngain * (hpreact - bnmeani) / bnstdi + bnbias
  with torch.no_grad(): # On ne veut pas calculer de gradient pour ces opérations
      bnmean_running = 0.999 * bnmean_running + 0.001 * bnmeani
      bnstd_running = 0.999 * bnstd_running + 0.001 * bnstdi
    
  h = torch.tanh(hpreact) 
  logits = h @ W2 + b2 
  loss = F.cross_entropy(logits, Yb)
  
  for p in parameters:
    p.grad = None
  loss.backward()
  lr = 0.1 if i < 100000 else 0.01 
  for p in parameters:
    p.data += -lr * p.grad
  if i % 10000 == 0:
    print(f'{i:7d}/{max_steps:7d}: {loss.item():.4f}')
  lossi.append(loss.log10().item())

      0/ 200000: 3.8241
  10000/ 200000: 1.9756
  20000/ 200000: 2.7151
  30000/ 200000: 2.3287
  40000/ 200000: 2.1411
  50000/ 200000: 2.3207
  60000/ 200000: 2.3250
  70000/ 200000: 2.0320
  80000/ 200000: 2.0615
  90000/ 200000: 2.2468
 100000/ 200000: 2.2081
 110000/ 200000: 2.1418
 120000/ 200000: 1.9665
 130000/ 200000: 1.8572
 140000/ 200000: 2.0577
 150000/ 200000: 2.1804
 160000/ 200000: 1.8604
 170000/ 200000: 1.9810
 180000/ 200000: 1.8228
 190000/ 200000: 1.9977

Consideraciones adicionales

Sesgo: La normalización por lotes normaliza las preactivaciones de los pesos. Esta normalización anula el sesgo (ya que este desplaza la distribución, mientras que nosotros la recentramos). Cuando se utiliza BatchNorm, se puede prescindir del sesgo. En la práctica, si se deja un sesgo, no causa problemas, pero es un parámetro de la red que será inútil.

Ubicación de BatchNorm: Según lo que hemos visto, es lógico colocar BatchNorm antes de la función de activación. En la práctica, algunos prefieren colocarla después de la capa de activación, por lo que no se sorprenda si se encuentra con esto en la literatura o en algún código.

Otras normalizaciones

Vamos a hacer un rápido repaso de las otras normalizaciones utilizadas para el entrenamiento de redes neuronales.

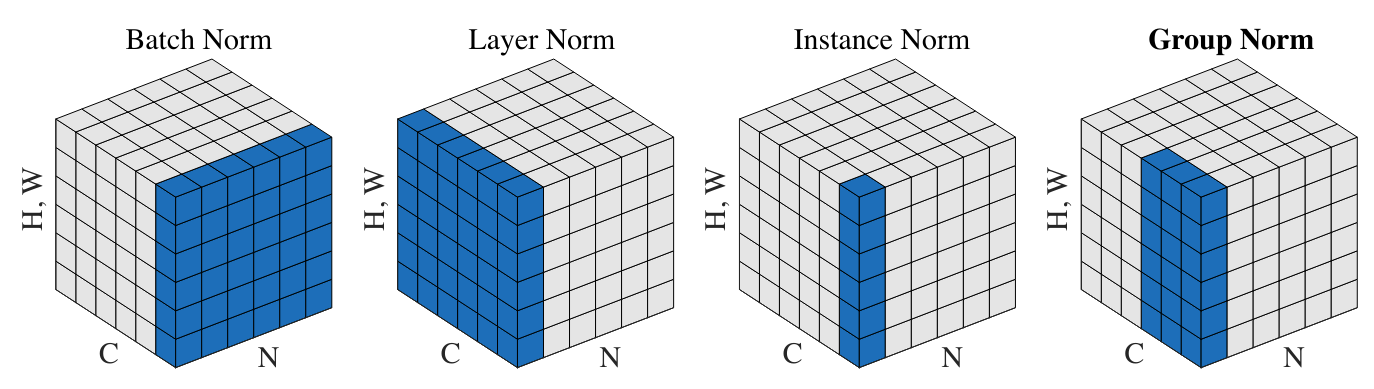
Figura extraída del artículo.

Normalización por Capa (Layer Normalization): Esta capa de normalización también se utiliza con mucha frecuencia, especialmente en modelos de lenguaje (GPT, Llama). Consiste en normalizar sobre el conjunto de activaciones de la capa en lugar de sobre la dimensión del batch. En nuestra implementación, esto simplemente implicaría cambiar:

# Batch normalization
bnmeani = hpreact.mean(0, keepdim=True)  
bnstdi = hpreact.std(0, keepdim=True)   
# Layer normalization
bnmeani = hpreact.mean(1, keepdim=True)  
bnstdi = hpreact.std(1, keepdim=True)  

Normalización por Instancia (Instance Normalization): Esta capa normaliza las activaciones en cada canal de cada elemento de manera independiente.

Normalización por Grupo (Group Normalization): Esta capa es una especie de fusión entre LayerNorm e InstanceNorm, ya que se calcula la normalización sobre grupos de canales (si el tamaño de un grupo es 1, es InstanceNorm, y si el tamaño de un grupo es \(C\), es LayerNorm).