Mi primer red neuronal#
En este curso, construiremos nuestra primera red neuronal utilizando la biblioteca micrograd. Micrograd es una biblioteca sencilla y fácil de entender, especializada en el cálculo automático de gradientes. Para dominarla mejor, puedes ver el vídeo de introducción de Andrej Karpathy (en inglés). Este cuaderno también se inspira en el cuaderno proporcionado en el repositorio de micrograd.
Construcción de una red neuronal con micrograd#
#!pip install micrograd # uncomment to install micrograd
import random
import numpy as np
import matplotlib.pyplot as plt
from micrograd.engine import Value
from micrograd.nn import Neuron, Layer, MLP
# Pour la reproducibilité
np.random.seed(1337)
random.seed(1337)
Para construir una red neuronal, primero necesitamos un problema que resolver. Para ello, utilizamos la función make_moons de scikit-learn, que permite generar un conjunto de datos. Para simplificar el cálculo de la pérdida (loss) en los pasos siguientes, reemplazamos las clases \(0\) y \(1\) por las clases \(-1\) y \(1\).
Inicialización del conjunto de datos#
from sklearn.datasets import make_moons, make_blobs
X, y = make_moons(n_samples=100, noise=0.1) # 100 éléments et un bruit Gaussien d'écart type 0.1 ajouté sur les données
print("Les données d'entrée sont de la forme : ",X[1])
y = y*2 - 1 # Pour avoir y=-1 ou y=1 (au lieu de 0 et 1)
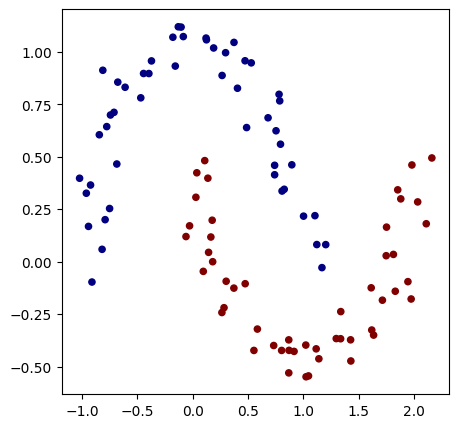
# Visualisation des données en 2D
plt.figure(figsize=(5,5))
plt.scatter(X[:,0], X[:,1], c=y, s=20, cmap='jet')
Les données d'entrée sont de la forme : [-0.81882941 0.05879006]
<matplotlib.collections.PathCollection at 0x177253e50>
Creación de la red neuronal#
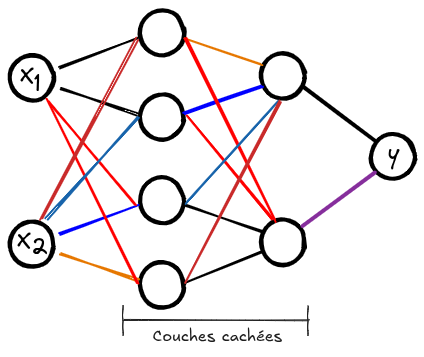
Ahora, inicializaremos nuestra red neuronal. Esta recibe \(2\) valores de entrada y debe producir una etiqueta \(-1\) o \(1\). La red que construiremos tiene \(2\) capas ocultas, cada una con \(16\) neuronas. Cada neurona funciona como una regresión logística, lo que convierte a nuestra red en un ensamblaje no lineal de múltiples regresiones logísticas.
A continuación, se muestra un esquema de la arquitectura de esta red:
# Initialisation du modèle
model = MLP(2, [16, 16, 1]) # Couches d'entrée de taille 2, deux couches cachées de 16 neurones et un neurone de sortie
print(model)
print("Nombre de paramètres", len(model.parameters()))
MLP of [Layer of [ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2), ReLUNeuron(2)], Layer of [ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16), ReLUNeuron(16)], Layer of [LinearNeuron(16)]]
Nombre de paramètres 337
Descenso de gradiente estocástico (SGD)#
Antes de continuar, hablemos sobre el descenso de gradiente estocástico (SGD). Para aplicar el algoritmo de descenso de gradiente en un conjunto de datos de tamaño \(N\), en teoría sería necesario calcular la pérdida y el gradiente en cada elemento antes de actualizar los pesos. Este método garantiza una disminución de la pérdida en cada iteración, pero es muy costoso para conjuntos de datos donde \(N\) es grande (a menudo \(N > 10^6\)). Además, sería necesario almacenar los gradientes de todos los \(N\) elementos en memoria, lo cual es imposible para grandes conjuntos de datos.
Para resolver este problema, utilizamos mini-batches, que son grupos de muestras del conjunto de datos. La optimización se realiza como en el descenso de gradiente clásico, pero la actualización de los pesos se realiza en cada mini-batch (por lo tanto, con mayor frecuencia). Esto hace que el proceso de optimización sea más rápido y permite manejar grandes cantidades de datos. El tamaño de un mini-batch se denomina batch size y su valor suele ser \(16\), \(32\) o \(64\). Para obtener más información sobre el descenso de gradiente estocástico, consulta Wikipedia o este artículo.
Definamos en Python una función para recuperar batch_size elementos aleatorios de nuestro conjunto de datos.
def get_batch(batch_size=64):
ri = np.random.permutation(X.shape[0])[:batch_size]
Xb, labels = X[ri], y[ri]
#inputs = [list(map(Value, xrow)) for xrow in Xb] # OLD
# Conversion des inputs en Value pour pouvoir utiliser micrograd
inputs = [list([Value(xrow[0]),Value(xrow[1])]) for xrow in Xb]
return inputs,labels
Función de pérdida#
Para entrenar nuestra red neuronal, debemos definir una función de pérdida (loss). En nuestro caso, tenemos dos clases y queremos maximizar el margen entre los ejemplos que pertenecen a clases diferentes. A diferencia de la pérdida de log-verosimilitud negativa utilizada previamente, buscamos maximizar esta diferencia, lo que hace que nuestro método sea más robusto ante nuevos elementos.
Utilizamos la pérdida de margen máximo (max-margin loss), definida por: \(\text{loss} = \max(0, 1 - y_i \cdot \text{score}_i)\)
def loss_function(scores,labels):
# La fonction .relu() prend le maximum entre 0 et la valeur de 1 - yi*scorei
losses = [(1 - yi*scorei).relu() for yi, scorei in zip(labels, scores)]
# On divise le loss par le nombre d'éléments du mini-batch
data_loss = sum(losses) * (1.0 / len(losses))
return data_loss
Entrenamiento del modelo#
Ahora que tenemos los elementos clave del entrenamiento, es hora de definir nuestro bucle de entrenamiento.
# Définissons nos hyper-paramètres d'entraînement
batch_size=128
iteration=50
Ahora podemos iniciar el entrenamiento de nuestro modelo:
for k in range(iteration):
# On récupère notre mini-batch random
inputs,labels=get_batch(batch_size=batch_size)
# On fait appel au modèle pour calculer les scores Y
scores = list(map(model, inputs))
# On calcule le loss
loss=loss_function(scores,labels)
accuracy = [(label > 0) == (scorei.data > 0) for label, scorei in zip(labels, scores)]
accuracy=sum(accuracy) / len(accuracy)
# Remise à zéro de valeurs de gradients avant de les calculer
model.zero_grad()
# Calcul des gradients grâce à l'autograd de micrograd
loss.backward()
# Mise à jour des poids avec les gradients calculés (SGD)
learning_rate = 1.0 - 0.9*k/100 # On diminue le learning rate au fur et à mesure de l'entraînement
for p in model.parameters():
p.data -= learning_rate * p.grad
if k % 1 == 0:
print(f"step {k} loss {loss.data}, accuracy {accuracy*100}%")
step 0 loss 0.8862514464368221, accuracy 50.0%
step 1 loss 1.7136790633950052, accuracy 81.0%
step 2 loss 0.733396126728699, accuracy 77.0%
step 3 loss 0.7615247055858604, accuracy 82.0%
step 4 loss 0.35978083334534205, accuracy 84.0%
step 5 loss 0.3039360355411295, accuracy 86.0%
step 6 loss 0.2716587340549048, accuracy 89.0%
step 7 loss 0.25896576803013205, accuracy 91.0%
step 8 loss 0.2468445503533517, accuracy 91.0%
step 9 loss 0.26038987927745966, accuracy 91.0%
step 10 loss 0.23569710047306525, accuracy 91.0%
step 11 loss 0.2403768930229477, accuracy 92.0%
step 12 loss 0.20603128479123115, accuracy 91.0%
step 13 loss 0.22061157796029193, accuracy 93.0%
step 14 loss 0.19010711228374735, accuracy 92.0%
step 15 loss 0.21687609382796402, accuracy 93.0%
step 16 loss 0.18642445342175254, accuracy 92.0%
step 17 loss 0.2064478196088666, accuracy 92.0%
step 18 loss 0.15299793102189654, accuracy 94.0%
step 19 loss 0.18164592701596197, accuracy 93.0%
step 20 loss 0.15209012673698674, accuracy 92.0%
step 21 loss 0.17985784886850317, accuracy 93.0%
step 22 loss 0.13186703020683818, accuracy 95.0%
step 23 loss 0.13971668862318976, accuracy 95.0%
step 24 loss 0.1052987732627048, accuracy 96.0%
step 25 loss 0.11575214222251122, accuracy 95.0%
step 26 loss 0.10138692709798285, accuracy 97.0%
step 27 loss 0.13983249990522056, accuracy 95.0%
step 28 loss 0.13439433831552547, accuracy 92.0%
step 29 loss 0.14946491199753797, accuracy 95.0%
step 30 loss 0.08058651087395295, accuracy 97.0%
step 31 loss 0.08894402478347964, accuracy 97.0%
step 32 loss 0.14846171628770516, accuracy 95.0%
step 33 loss 0.08534324122933533, accuracy 97.0%
step 34 loss 0.06930425973662234, accuracy 97.0%
step 35 loss 0.10224309625633382, accuracy 95.0%
step 36 loss 0.05690038135075194, accuracy 97.0%
step 37 loss 0.04361190103707672, accuracy 97.0%
step 38 loss 0.04085954349889362, accuracy 98.0%
step 39 loss 0.06115860793647568, accuracy 97.0%
step 40 loss 0.06712605274368717, accuracy 99.0%
step 41 loss 0.1007776535938798, accuracy 95.0%
step 42 loss 0.047219615684323896, accuracy 97.0%
step 43 loss 0.03229533112572595, accuracy 99.0%
step 44 loss 0.028346610758982437, accuracy 99.0%
step 45 loss 0.05011775341000794, accuracy 99.0%
step 46 loss 0.09321634150737651, accuracy 96.0%
step 47 loss 0.055859575569553566, accuracy 98.0%
step 48 loss 0.02709965160774589, accuracy 99.0%
step 49 loss 0.054945465674614925, accuracy 98.0%
Como pueden observar, la pérdida (loss) no disminuye sistemáticamente en cada paso del entrenamiento. Esto se explica por el descenso de gradiente estocástico: el hecho de no considerar todo el conjunto de datos en cada iteración introduce un componente aleatorio. Sin embargo, la pérdida disminuye en promedio durante el entrenamiento, lo que permite obtener un modelo robusto más rápidamente.
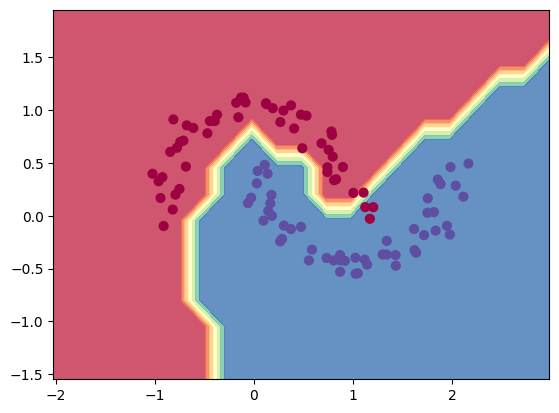
# Visualisation de la frontière de décision
h = 0.25
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Xmesh = np.c_[xx.ravel(), yy.ravel()]
inputs = [list(map(Value, xrow)) for xrow in Xmesh]
scores = list(map(model, inputs))
Z = np.array([s.data > 0 for s in scores])
Z = Z.reshape(xx.shape)
fig = plt.figure()
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
(-1.548639298268643, 1.951360701731357)