Activaciones e inicializaciones

En este curso, retomaremos el modelo Fully Connected presentado en el curso 5 sobre PNL (Procesamiento del Lenguaje Natural). Analizaremos el comportamiento de las activaciones a lo largo de la red durante su inicialización. Este contenido está inspirado en la clase de Andrej Karpathy titulada Building makemore Part 3: Activations & Gradients, BatchNorm.

Las redes neuronales ofrecen varias ventajas:

• Son muy flexibles y pueden resolver una amplia variedad de problemas.

• Su implementación es relativamente sencilla.

Sin embargo, su optimización suele ser compleja, especialmente cuando se trata de redes profundas.

Recuperación de código

Estamos usando el código del cuaderno 3 del curso 5 sobre PNL.

import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
%matplotlib inline

words = open('../05_NLP/prenoms.txt', 'r').read().splitlines()
chars = sorted(list(set(''.join(words))))
stoi = {s:i+1 for i,s in enumerate(chars)}
stoi['.'] = 0
itos = {i:s for s,i in stoi.items()}

Por razones pedagógicas, no utilizaremos el dataset ni el dataloader de PyTorch. En su lugar, evaluaremos la pérdida (loss) al inicio del entrenamiento, tras procesar el primer batch. El procedimiento es similar al estándar, con una diferencia clave: en cada iteración, seleccionamos un batch aleatorio en lugar de recorrer todo el dataset en cada epoch.

block_size = 3 # Contexte

def build_dataset(words):  
  X, Y = [], []
  
  for w in words:
    context = [0] * block_size
    for ch in w + '.':
      ix = stoi[ch]
      X.append(context)
      Y.append(ix)
      context = context[1:] + [ix] 

  X = torch.tensor(X)
  Y = torch.tensor(Y)
  print(X.shape, Y.shape)
  return X, Y

import random
random.seed(42)
random.shuffle(words)
n1 = int(0.8*len(words))
n2 = int(0.9*len(words))

Xtr,  Ytr  = build_dataset(words[:n1])     # 80%
Xdev, Ydev = build_dataset(words[n1:n2])   # 10%
Xte,  Yte  = build_dataset(words[n2:])     # 10%

torch.Size([180834, 3]) torch.Size([180834])
torch.Size([22852, 3]) torch.Size([22852])
torch.Size([22639, 3]) torch.Size([22639])

embed_dim=10 # Dimension de l'embedding de C
hidden_dim=200 # Dimension de la couche cachée

C = torch.randn((46, embed_dim))
W1 = torch.randn((block_size*embed_dim, hidden_dim))
b1 = torch.randn(hidden_dim)
W2 = torch.randn((hidden_dim, 46))
b2 = torch.randn(46)
parameters = [C, W1, b1, W2, b2]
for p in parameters:
  p.requires_grad = True

max_steps = 200000
batch_size = 32
lossi = []

for i in range(max_steps):
  # Permet de construire un mini-batch
  ix = torch.randint(0, Xtr.shape[0], (batch_size,))
  
  # Forward
  Xb, Yb = Xtr[ix], Ytr[ix] 
  emb = C[Xb] 
  embcat = emb.view(emb.shape[0], -1)
  hpreact = embcat @ W1 + b1 

  h = torch.tanh(hpreact) 
  logits = h @ W2 + b2 
  loss = F.cross_entropy(logits, Yb)
  
  # Retropropagation
  for p in parameters:
    p.grad = None
  
  loss.backward()
  # Mise à jour des paramètres
  lr = 0.1 if i < 100000 else 0.01 # On descend le learning rate d'un facteur 10 après 100000 itérations
  for p in parameters:
    p.data += -lr * p.grad

  if i % 10000 == 0:
    print(f'{i:7d}/{max_steps:7d}: {loss.item():.4f}')
  lossi.append(loss.log10().item())

      0/ 200000: 21.9772
  10000/ 200000: 2.9991
  20000/ 200000: 2.5258
  30000/ 200000: 1.9657
  40000/ 200000: 2.4326
  50000/ 200000: 1.7670
  60000/ 200000: 2.1324
  70000/ 200000: 2.4160
  80000/ 200000: 2.2237
  90000/ 200000: 2.3905
 100000/ 200000: 1.9304
 110000/ 200000: 2.1710
 120000/ 200000: 2.3444
 130000/ 200000: 2.0970
 140000/ 200000: 1.8623
 150000/ 200000: 1.9792
 160000/ 200000: 2.4602
 170000/ 200000: 2.0968
 180000/ 200000: 2.0466
 190000/ 200000: 2.3746

plt.plot(lossi)

[<matplotlib.lines.Line2D at 0x7f028467b990>]

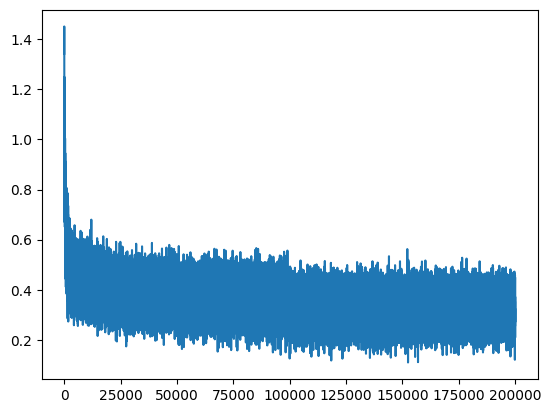
Hay mucho “ruido” en los resultados, ya que calculamos la pérdida (loss) en batches pequeños en comparación con el conjunto completo de datos de entrenamiento.

Pérdida anormalmente alta en la inicialización

El entrenamiento transcurre correctamente. No obstante, observamos algo anómalo: la pérdida inicial (loss) es excesivamente alta. Lo esperado sería un valor equivalente a un escenario donde cada letra tenga una probabilidad uniforme de aparición (es decir, \(p = \frac{1}{46}\)).

En este caso, el negative log likelihood sería: \(-ln\left(\frac{1}{46}\right) = 3.83\)

Por lo tanto, sería lógico obtener un valor cercano a este en el primer cálculo de loss.

Pequeño ejemplo que ilustra el problema

Para entender qué está ocurriendo, utilicemos un ejemplo sencillo y analicemos los valores de loss según la inicialización. Supongamos que todos los pesos en logits se inicializan en 0. En este caso, obtendríamos probabilidades uniformes.

logits=torch.tensor([0.0,0.0,0.0,0.0])
probs=torch.softmax(logits,dim=0)
loss= -probs[1].log()
probs,loss

(tensor([0.2500, 0.2500, 0.2500, 0.2500]), tensor(1.3863))

Sin embargo, no es recomendable inicializar los pesos de una red neuronal en 0. En su lugar, hemos utilizado una inicialización aleatoria basada en una distribución gaussiana estándar (media = 0, desviación estándar = 1).

logits=torch.randn(4)
probs=torch.softmax(logits,dim=0)
loss= -probs[1].log()
probs,loss

(tensor([0.3143, 0.0607, 0.3071, 0.3178]), tensor(2.8012))

El problema es evidente: el azar de la distribución gaussiana desequilibra los valores hacia un extremo u otro (puedes ejecutar el código anterior varias veces para verificarlo).

¿Cómo solucionarlo? Basta con multiplicar nuestro vector logit por un valor pequeño (ej. 0.01) para reducir la magnitud inicial de los pesos y lograr que la salida de softmax sea más uniforme.

logits=torch.randn(4)*0.01
probs=torch.softmax(logits,dim=0)
loss= -probs[1].log()
probs,loss

(tensor([0.2489, 0.2523, 0.2495, 0.2493]), tensor(1.3772))

Obtenemos un valor de loss muy cercano al esperado para probabilidades uniformes.

Nota: En cambio, sí es válido inicializar los sesgos (bias) en 0, ya que no tiene sentido asignarles un valor positivo o negativo al inicio.

Entrenamiento con ajuste de inicialización

Retomemos el código anterior, pero aplicando los nuevos valores de inicialización.

C = torch.randn((46, embed_dim))
W1 = torch.randn((block_size*embed_dim, hidden_dim))*0.01 # On initialise les poids à une petite valeur
b1 = torch.randn(hidden_dim) *0 # On initialise les biais à 0
W2 = torch.randn((hidden_dim, 46))*0.01
b2 = torch.randn(46)*0 
parameters = [C, W1, b1, W2, b2]
for p in parameters:
  p.requires_grad = True

lossi = []

for i in range(max_steps):
  ix = torch.randint(0, Xtr.shape[0], (batch_size,))
  Xb, Yb = Xtr[ix], Ytr[ix] 
  emb = C[Xb] 
  embcat = emb.view(emb.shape[0], -1)
  hpreact = embcat @ W1 + b1 
  h = torch.tanh(hpreact) 
  logits = h @ W2 + b2 
  loss = F.cross_entropy(logits, Yb)
  
  for p in parameters:
    p.grad = None
  loss.backward()
  lr = 0.1 if i < 100000 else 0.01 
  for p in parameters:
    p.data += -lr * p.grad
  if i % 10000 == 0:
    print(f'{i:7d}/{max_steps:7d}: {loss.item():.4f}')
  lossi.append(loss.log10().item())

      0/ 200000: 3.8304
  10000/ 200000: 2.4283
  20000/ 200000: 2.0651
  30000/ 200000: 2.1124
  40000/ 200000: 2.3158
  50000/ 200000: 2.2752
  60000/ 200000: 2.1887
  70000/ 200000: 2.1783
  80000/ 200000: 1.8120
  90000/ 200000: 2.3178
 100000/ 200000: 2.0973
 110000/ 200000: 1.8992
 120000/ 200000: 1.6917
 130000/ 200000: 2.2747
 140000/ 200000: 1.8054
 150000/ 200000: 2.3569
 160000/ 200000: 2.4231
 170000/ 200000: 2.0711
 180000/ 200000: 2.1379
 190000/ 200000: 1.8419

plt.plot(lossi)

[<matplotlib.lines.Line2D at 0x7f0278310110>]

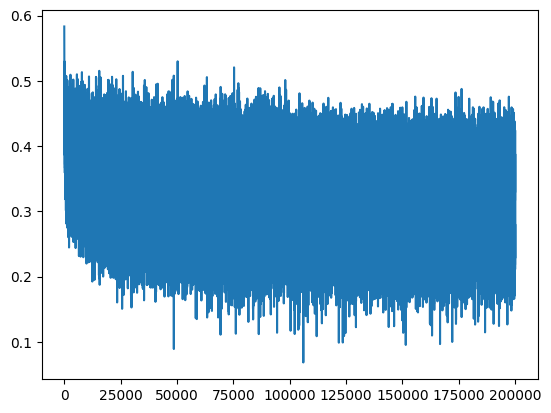
Ahora obtenemos una curva de pérdida (loss) que no parte de un valor anómalo, lo que acelera significativamente el proceso de optimización.

Otro problema

Podría pensarse que un loss elevado no es necesariamente un problema. Sin embargo, una mala inicialización de los pesos puede generar otros inconvenientes.

Analicemos la primera iteración del entrenamiento con valores inicializados sin el factor 0.01.

C = torch.randn((46, embed_dim))
W1 = torch.randn((block_size*embed_dim, hidden_dim)) 
b1 = torch.randn(hidden_dim) 
W2 = torch.randn((hidden_dim, 46))
b2 = torch.randn(46)
parameters = [C, W1, b1, W2, b2]
for p in parameters:
  p.requires_grad = True

ix = torch.randint(0, Xtr.shape[0], (batch_size,))
Xb, Yb = Xtr[ix], Ytr[ix] 
emb = C[Xb] 
embcat = emb.view(emb.shape[0], -1)
hpreact = embcat @ W1 + b1 
h = torch.tanh(hpreact) 
logits = h @ W2 + b2 
loss = F.cross_entropy(logits, Yb)
  
for p in parameters:
  p.grad = None
loss.backward()

Observamos el histograma de valores después de la función de activación tanh.

plt.hist(h.view(-1).tolist(),50);

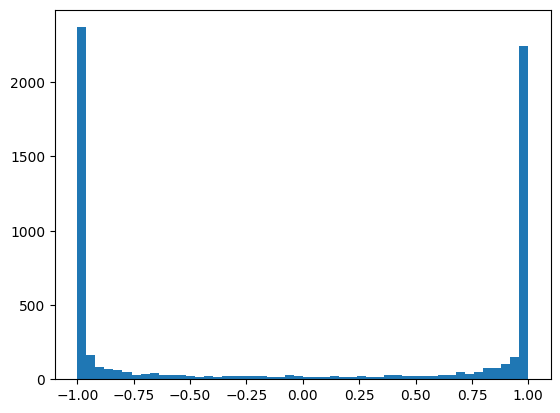
Observamos que la mayoría de los valores se concentran alrededor de 1 o -1.

¿Por qué es esto un problema? Durante el cálculo del gradiente, al aplicar la regla de la cadena, multiplicamos los gradientes de las distintas etapas. La derivada de la función tanh es: \(tanh'(t) = 1 - t^2\)

Si los valores de \(t\) están cerca de 1 o -1, el gradiente será extremadamente pequeño (nunca cero, pues es una asíntota). Esto implica que el gradiente no se propaga correctamente, dificultando la optimización al inicio del entrenamiento.

plt.figure(figsize=(20,10))
plt.imshow(h.abs()>0.99,cmap='gray',interpolation='nearest')

<matplotlib.image.AxesImage at 0x7f02780ae550>

Cada punto blanco representa un neurona cuyo gradiente es aproximadamente 0.

Neurona muerta: Si una de estas columnas estuviera completamente en blanco, significaría que la neurona no se activa para ningún elemento del batch. Esto implica que se trata de una neurona inútil, sin impacto en el resultado y que no puede optimizarse con los valores actuales del batch.

Notas importantes:

• Este comportamiento no es exclusivo de tanh: funciones como sigmoid y ReLU también pueden presentarlo.

• El problema no impidió entrenar correctamente nuestra red, ya que se trata de un modelo pequeño. En redes más profundas, es un problema grave, y se recomienda verificar las activaciones en las distintas capas.

• Las neuronas muertas pueden aparecer durante la inicialización o durante el entrenamiento (por ejemplo, si el learning rate es demasiado alto).

¿Como solucionar este problema?

Afortunadamente, este problema puede resolverse de la misma manera que el del loss demasiado elevado. Para confirmarlo, analicemos los valores de las activaciones y las neuronas inactivas al inicio, aplicando los nuevos valores de inicialización.

C = torch.randn((46, embed_dim))
W1 = torch.randn((block_size*embed_dim, hidden_dim)) *0.01# On initialise les poids à une petite valeur
b1 = torch.randn(hidden_dim) *0 # On initialise les biais à 0
W2 = torch.randn((hidden_dim, 46)) *0.01
b2 = torch.randn(46)*0 
parameters = [C, W1, b1, W2, b2]
for p in parameters:
  p.requires_grad = True

ix = torch.randint(0, Xtr.shape[0], (batch_size,))
Xb, Yb = Xtr[ix], Ytr[ix] 
emb = C[Xb] 
embcat = emb.view(emb.shape[0], -1)
hpreact = embcat @ W1 + b1 
h = torch.tanh(hpreact) 
logits = h @ W2 + b2 
loss = F.cross_entropy(logits, Yb)
  
for p in parameters:
  p.grad = None
loss.backward()

plt.hist(h.view(-1).tolist(),50);

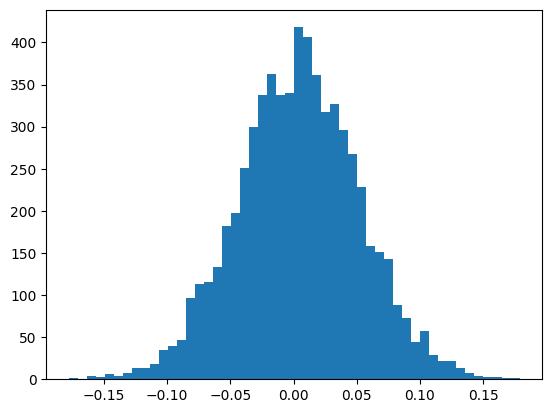
plt.figure(figsize=(20,10))
plt.imshow(h.abs()>0.99,cmap='gray',interpolation='nearest')

<matplotlib.image.AxesImage at 0x7f025c538190>

¡Todo funciona correctamente ahora!

Valores óptimos en la inicialización

Dada la importancia de este problema, numerosas investigaciones se han enfocado en él. Una publicación destacada es Delving Deep into Rectifiers, que introduce la inicialización de Kaiming. Este trabajo propone valores de inicialización específicos para cada función de activación, garantizando una distribución centrada y reducida en toda la red.

Este método está implementado en PyTorch, y las capas que creemos en PyTorch se inicializan automáticamente de esta manera.

¿Por qué este curso está en los bonos cuando parece muy importante?

Este problema es, efectivamente, un desafío clave. Sin embargo, al usar PyTorch, todos los parámetros ya se inicializan correctamente, por lo que no suele ser necesario modificarlos manualmente.

Además, se han propuesto diversas técnicas para mitigar este problema, entre las que destacan:

• Batch Normalization (Batch Norm): Normaliza los valores antes de la activación en cada capa de la red (se abordará en el siguiente notebook).

• Conexiones residuales (Residual Connections): Permiten propagar el gradiente a través de toda la red sin que este se vea afectado en exceso por las funciones de activación.

Aunque estas consideraciones son fundamentales, en la práctica no es estrictamente necesario dominarlas para entrenar una red neuronal, gracias a las optimizaciones ya integradas en frameworks como PyTorch.