Autoencoders variacionales#
En este curso, te presentamos los autoencoders variacionales (VAE, por sus siglas en inglés). Comenzamos con un breve repaso del curso 4 sobre autoencoders y luego introducimos el uso de los VAE como modelos generativos. Este curso se inspira en una publicación de blog y no profundiza en los detalles matemáticos del funcionamiento del VAE. Las figuras utilizadas en este notebook también provienen de la publicación de blog.
Repaso sobre los autoencoders#
Un autoencoder es una red neuronal con forma de reloj de arena. Está compuesto por un encoder que codifica la información en un espacio latente de dimensión reducida y un decoder que reconstruye los datos originales a partir de la representación latente.
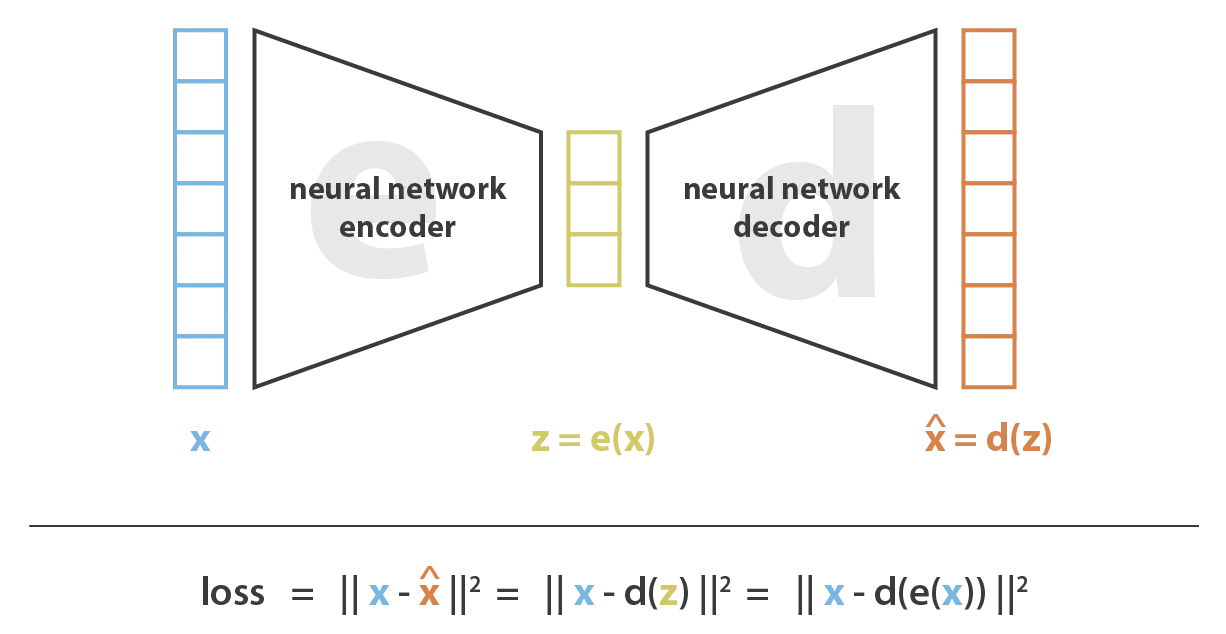
Los autoencoders pueden utilizarse para muchas aplicaciones, pero su función principal es la compresión de datos. Este método de compresión emplea la optimización mediante el algoritmo de descenso de gradiente.
Intuición#
Imagina que el espacio latente de nuestro decoder es regular (representado por una distribución de probabilidad conocida). En este caso, podríamos muestrear un elemento aleatorio de esta distribución para generar nuevos datos. Sin embargo, en un autoencoder clásico, la representación latente no es regular, por lo que es imposible usarla para generar datos.
Al reflexionar sobre esto, tiene sentido: la función de pérdida (loss) del autoencoder se basa únicamente en la calidad de la reconstrucción y no impone restricciones sobre la forma del espacio latente.
Por lo tanto, nos gustaría imponer una estructura al espacio latente del autoencoder para poder generar nuevos datos a partir de él.
Autoencoder variacional#
Un autoencoder variacional (VAE) es un tipo de autoencoder que está diseñado para tener un espacio latente que permita generar datos. Su entrenamiento está regulado para alcanzar este objetivo.
La idea principal es codificar la entrada (input) como una distribución de probabilidad en lugar de un único valor (como en un autoencoder clásico). En la práctica, el encoder predice dos parámetros que definen una distribución normal: la media (\(\mu\)) y la varianza (\(\sigma^2\)).
Durante el entrenamiento, el VAE funciona de la siguiente manera:
El encoder transforma la entrada en una distribución de probabilidad, prediciendo \(\mu\) y \(\sigma^2\).
Se muestrean valores a partir de la distribución gaussiana definida por \(\mu\) y \(\sigma^2\).
El decoder reconstruye los datos originales a partir del valor muestreado.
Se aplica backpropagation para actualizar los pesos del modelo.
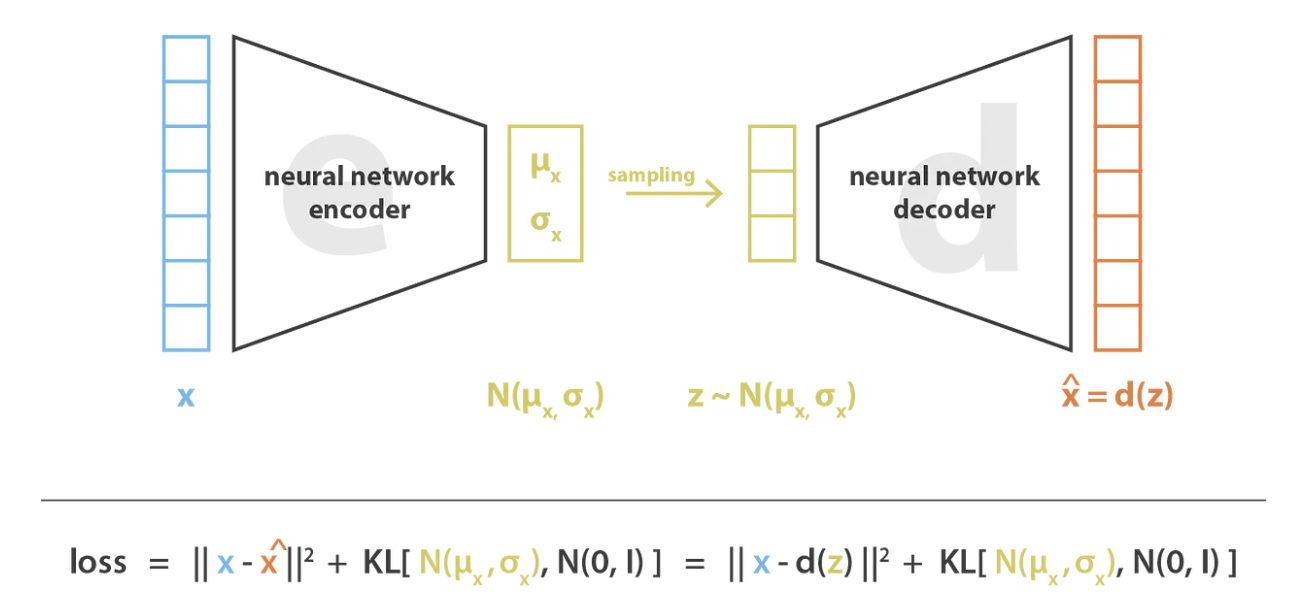
Para asegurar que el entrenamiento cumpla con el objetivo deseado, es necesario añadir un término a la función de pérdida (loss): la divergencia de Kullback-Leibler. Este término fuerza a que la distribución del espacio latente se aproxime a una distribución normal estándar (centrada y reducida).
Para generar datos coherentes, se deben considerar dos propiedades clave:
Continuidad: Puntos cercanos en el espacio latente deben producir datos similares en el espacio de salida.
Completitud: Los puntos decodificados deben ser significativos y válidos en el espacio de salida.
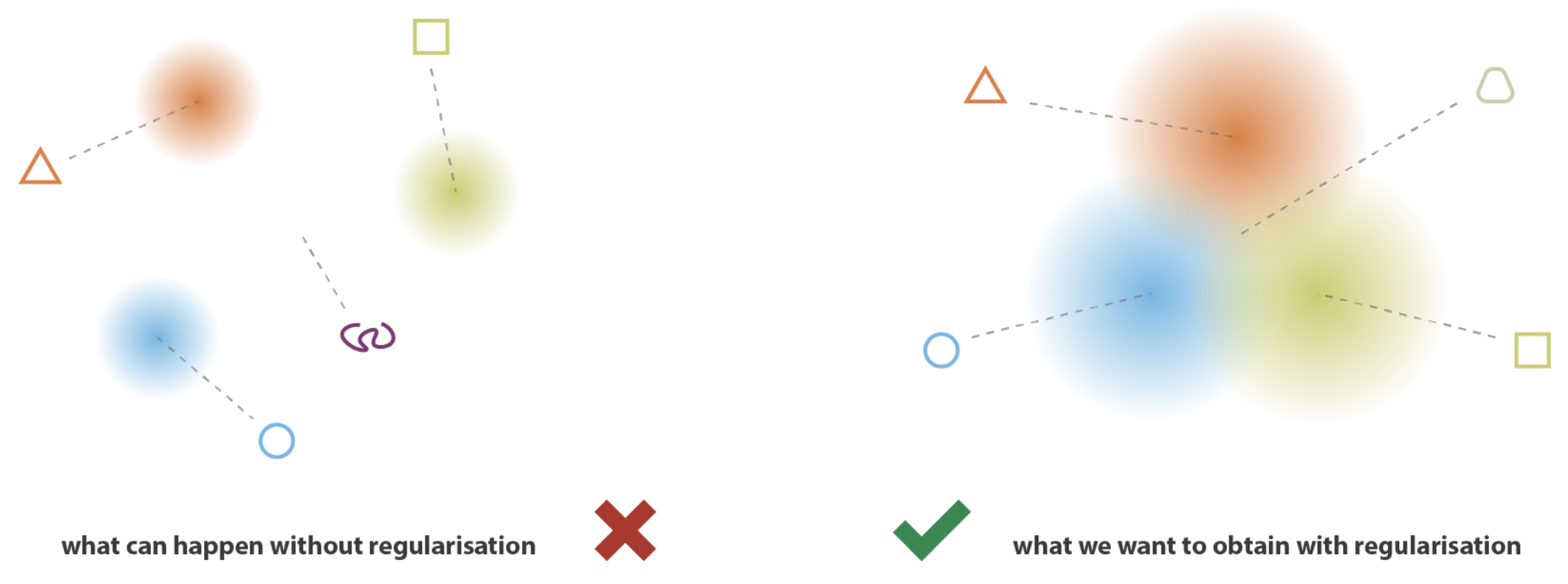
La divergencia de Kullback-Leibler garantiza estas dos propiedades. Si solo se utilizara la función de pérdida de reconstrucción, el VAE podría comportarse como un autoencoder clásico, prediciendo varianzas casi nulas (lo que equivaldría a un único punto, similar a lo que predice un encoder en un AE).
La divergencia de Kullback-Leibler fomenta que las distribuciones en el espacio latente sean similares entre sí, lo que permite generar datos coherentes al realizar el muestreo.
Nota: Existe un importante fundamento teórico detrás de los autoencoders variacionales, pero no se profundizará en él en este curso. Si deseas aprender más, puedes consultar el curso CS236 de Stanford, en particular este enlace.