Introducción a PyTorch

Introducción a PyTorch#

Este notebook comienza con una introducción a PyTorch, una biblioteca muy popular en el campo del deep learning. Retomaremos la red neuronal del notebook anterior e implementaremos su funcionalidad en PyTorch.

import random
import numpy as np 
import matplotlib.pyplot as plt

# Import classiques des utilisateurs de pytorch 
import torch 
import torch.nn as nn
import torch.nn.functional as F

Conjunto de datos y DataLoader#

Vamos a reconstruir un conjunto de datos de manera similar al notebook anterior. Además, debemos convertir las variables \(X\) e \(y\) en tensores (equivalente a Value en micrograd).

# Initialisation du dataset 
from sklearn.datasets import make_moons

X, y = make_moons(n_samples=100, noise=0.1)
X=torch.tensor(X).float() # Conversion en tensor pytorch (équivalent de Value)
y=torch.tensor(y).float() # Conversion en tensor pytorch
y = y*2 - 1 

plt.figure(figsize=(5,5))
plt.scatter(X[:,0], X[:,1], c=y, s=20, cmap='jet')

<matplotlib.collections.PathCollection at 0x7c6677d37350>
../_images/4bd5c0637bd91b6edc22e5b405f8c15853ee00a6168f91f0fab3cfde16b99d51.png

Ahora, utilicemos las funcionalidades de PyTorch para crear nuestro conjunto de datos y nuestro DataLoader. El conjunto de datos agrupa simplemente las entradas y las etiquetas, mientras que el DataLoader facilita el uso del descenso de gradiente estocástico al proporcionar directamente un mini-batch de datos aleatorios extraídos del conjunto (el DataLoader actúa como un iterador).

from torch.utils.data import TensorDataset, DataLoader
# Création d'un dataset qui stocke les couples de valeurs X,y
dataset = TensorDataset(X, y)

# Création d'un dataloader qui permet de gérer automatiquement les mini-batchs pour la descente de gradient stochastique. 
dataloader = DataLoader(dataset, batch_size=32, shuffle=True)

Para aprender más sobre el conjunto de datos y el DataLoader, puedes consultar la documentación de PyTorch.

Construcción del modelo#

Ahora, construyamos nuestro modelo con 2 capas ocultas.

Para ello, crearemos una clase MLP que herede de la clase nn.Module. Luego, construimos las capas de la red utilizando la función nn.Linear(in_features, out_features), que crea una capa completamente conectada que recibe in_features como entrada y devuelve out_features como salida. Se trata de una capa compuesta por out_features neuronas conectadas a in_features entradas.

class mlp(nn.Module):
  def __init__(self, *args, **kwargs) -> None:
    super().__init__(*args, **kwargs)
    self.fc1=nn.Linear(2,16) # première couche cachée 
    self.fc2=nn.Linear(16,16) # seconde couche cachée 
    self.fc3=nn.Linear(16,1) # couche de sortie
  
  # La fonction forward est la fonction appelée lorsqu'on fait model(x)
  def forward(self,x):
    x=F.relu(self.fc1(x)) # le F.relu permet d'appliquer la fonction d'activation ReLU sur la sortie de notre couche 
    x=F.relu(self.fc2(x))
    output=self.fc3(x)
    return output

model = mlp() # Couches d'entrée de taille 2, deux couches cachées de 16 neurones et un neurone de sortie
print(model)
print("Nombre de paramètres", sum(p.numel() for p in model.parameters()))

mlp(
  (fc1): Linear(in_features=2, out_features=16, bias=True)
  (fc2): Linear(in_features=16, out_features=16, bias=True)
  (fc3): Linear(in_features=16, out_features=1, bias=True)
)
Nombre de paramètres 337

Observamos que tenemos el mismo número de parámetros que en el notebook anterior, donde utilizamos micrograd.

Función de pérdida#

En PyTorch, ciertas funciones de pérdida ya están implementadas en la biblioteca. Antes de implementar tu propia función, verifica si ya existe.

Aquí, utilizaremos la función torch.nn.MSELoss de PyTorch. Se trata de la siguiente pérdida: \(\text{MSE}(y, \hat{y}) = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2\) donde \(y_i\) es el valor real (etiqueta), \(\hat{y}_i\) es el valor predicho y \(n\) es el número total de ejemplos en el mini-batch.

En PyTorch, esta función de pérdida se implementa fácilmente:

criterion=torch.nn.MSELoss()

Entrenamiento#

Para el entrenamiento, definamos los hiperparámetros y el optimizer. El optimizer es una clase de PyTorch que especifica el método de actualización de los pesos durante el entrenamiento (actualización de los pesos del modelo y tasa de aprendizaje). Existen varios optimizers: SGD, Adam, Adagrad, RMSProp, etc. Utilizamos SGD (Stochastic Gradient Descent) para reproducir las condiciones de entrenamiento del notebook anterior, pero en la práctica, a menudo se prefiere usar Adam (Adaptive Moment Estimation). Para saber más sobre los optimizers y sus diferencias, puedes consultar el curso adicional sobre optimizers, la documentación de PyTorch o este artículo.

# Hyper-paramètres
epochs = 100 # Nombre de fois où l'on parcoure l'ensemble des données d'entraînement
learning_rate=0.1
optimizer=torch.optim.SGD(model.parameters(),lr=learning_rate)

/home/aquilae/anaconda3/envs/dev/lib/python3.11/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
  from .autonotebook import tqdm as notebook_tqdm

También podemos utilizar un scheduler que modifica el valor de la tasa de aprendizaje durante el entrenamiento. Esto puede acelerar la convergencia al comenzar con una tasa de aprendizaje alta y reducirla progresivamente. Para obtener una tasa de aprendizaje que disminuya durante el entrenamiento, como en el ejemplo de micrograd, podemos usar LinearLR. Para saber más sobre los diferentes tipos de schedulers, puedes consultar la documentación de PyTorch.

scheduler=torch.optim.lr_scheduler.LinearLR(optimizer=optimizer,start_factor=1,end_factor=0.05)

for i in range(epochs):
  loss_epoch=0
  accuracy=[]
  for batch_X, batch_y in dataloader:
    scores=model(batch_X)        
    loss=criterion(scores,batch_y.unsqueeze(1))
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    #scheduler.step() # Pour activer le scheduler  
    loss_epoch+=loss
    
    accuracy += [(label > 0) == (scorei.data > 0) for label, scorei in zip(batch_y, scores)]
  accuracy=sum(accuracy) / len(accuracy) 
  
  if i % 10 == 0:
    print(f"step {i} loss {loss_epoch}, précision {accuracy*100}%")

step 0 loss 0.12318143993616104, précision tensor([100.])%
step 10 loss 0.1347985863685608, précision tensor([100.])%
step 20 loss 0.10458286106586456, précision tensor([100.])%
step 30 loss 0.14222581684589386, précision tensor([100.])%
step 40 loss 0.1081438660621643, précision tensor([100.])%
step 50 loss 0.10838648676872253, précision tensor([100.])%
step 60 loss 0.09485019743442535, précision tensor([100.])%
step 70 loss 0.07788567245006561, précision tensor([100.])%
step 80 loss 0.10796503722667694, précision tensor([100.])%
step 90 loss 0.07869727909564972, précision tensor([100.])%

¡El entrenamiento es mucho más rápido!

Podemos visualizar los resultados en nuestros datos:

h = 0.25
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))
Xmesh = np.c_[xx.ravel(), yy.ravel()]

inputs=torch.tensor(Xmesh).float()
scores=model(inputs)

Z = np.array([s.data > 0 for s in scores])
Z = Z.reshape(xx.shape)

fig = plt.figure()
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())

(-1.6418534517288208, 2.108146548271179)
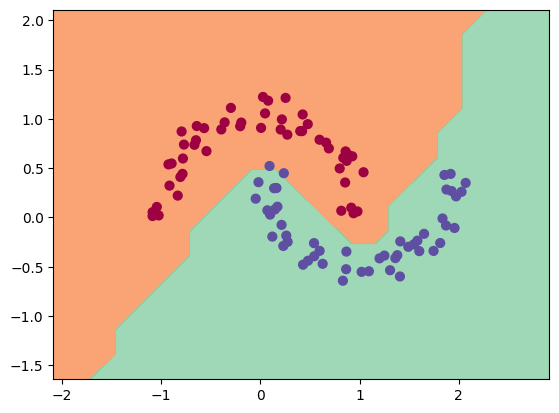
../_images/29e5f5c65a34be50e175ff381f354dc1df0c9076595efd9d3b482cba0112bb3a.png

Como pueden observar, el entrenamiento se ha desarrollado correctamente y hemos logrado una buena separación de los datos.

Contents