Redes neuronales recurrentes

Redes neuronales recurrentes#

En este curso, exploraremos las redes neuronales recurrentes (RNN) para predecir el siguiente carácter. Nos basamos en la arquitectura descrita en el artículo Recurrent neural network based language model, que propone una versión simplificada de RNN para esta tarea.

Ventaja clave: a diferencia de los modelos basados en redes fully connected (vistos anteriormente), los RNN no requieren un tamaño de contexto fijo.

Los RNN mantenienen en memoria el contexto, independientemente de la longitud de la secuencia. Aunque esto suena prometedor en teoría, veremos al final del curso que tienen limitaciones prácticas.

RNN

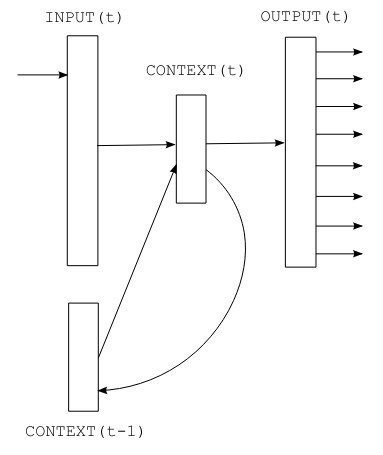
Figura extraída del artículo original.

¿Cómo funciona una RNN?#

Las RNN procesan los datos de forma secuencial: los caracteres se analizan uno a uno. El carácter siguiente depende tanto del elemento actual como del estado oculto (\(s\)), que almacena información de los caracteres anteriores.

Componentes matemáticos (en un instante \(t\)):

  • Entrada (\(x\)): combinación del one-hot encoding del carácter actual (\(w(t)\)) y el estado previo (\(s(t-1)\)). \(x(t) = w(t) + s(t-1)\)

  • Estado oculto (\(s\)): se actualiza aplicando la función sigmoide a la entrada. \(s(t) = sigmoid(x(t))\)

  • Salida (\(y\)): probabilidades de los caracteres siguientes, calculadas con softmax. \(y(t) = softmax(s(t))\)

Parámetro clave: el tamaño de la capa oculta (\(s\)). Inicialización: \(s(0)\) suele ser un vector pequeño (ej. ceros o valores aleatorios).

Aplicación práctica#

import torch
import torch.nn as nn

El conjunto de datos#

Generar nombres de pila con una RNN no es muy útil, ya que son cortos y el contexto es limitado. Para tareas más interesantes, necesitamos un conjunto de datos con un contexto más amplio.

Usaremos un archivo de texto con los diálogos de Molière, creado a partir de sus obras completas disponibles en Gutenberg.org. Los datos se limpiaron para conservar solo los diálogos.

with open('moliere.txt', 'r', encoding='utf-8') as f:
    text = f.read()
print("Nombre de caractères dans le dataset : ", len(text))

Nombre de caractères dans le dataset :  1687290

Dado que el conjunto de datos es grande, utilizaremos solo una parte (por ejemplo, los primeros 50,000 caracteres) para agilizar el procesamiento.

text=text[:50000]
print("Nombre de caractères dans le dataset : ", len(text))

Nombre de caractères dans le dataset :  50000

Primeros 250 caracteres del conjunto de datos:

print(text[:250])

VALÈRE.

Eh bien, Sabine, quel conseil me donnes-tu?

SABINE.

Vraiment, il y a bien des nouvelles. Mon oncle veut résolûment que ma
cousine épouse Villebrequin, et les affaires sont tellement avancées,
que je crois qu'ils eussent été mariés dès aujo

Número de caracteres únicos en el dataset:

chars = sorted(list(set(text)))
vocab_size = len(chars)
print(''.join(chars))
print("Nombre de caractères différents : ", vocab_size)

 !'(),-.:;?ABCDEFGHIJLMNOPQRSTUVYabcdefghijlmnopqrstuvxyzÇÈÉàâæçèéêîïôùû
Nombre de caractères différents :  73

Creamos un mapeo bidireccional entre caracteres y enteros.

stoi = { ch:i for i,ch in enumerate(chars) }
itos = { i:ch for i,ch in enumerate(chars) }
encode = lambda s: [stoi[c] for c in s] # encode : prend un string et output une liste d'entiers
decode = lambda l: ''.join([itos[i] for i in l]) # decode: prend une liste d'entiers et output un string

Codificamos el dataset:

  1. Convertimos las cadenas de caracteres a enteros.

  2. Transformamos los enteros en tensores de PyTorch.

data = torch.tensor(encode(text), dtype=torch.long)
print(data[:250]) # Les 250 premiers caractères encodé

tensor([32, 12, 22, 59, 28, 16,  8,  0,  0, 16, 41,  1, 35, 42, 38, 46,  6,  1,
        29, 34, 35, 42, 46, 38,  6,  1, 49, 53, 38, 44,  1, 36, 47, 46, 51, 38,
        42, 44,  1, 45, 38,  1, 37, 47, 46, 46, 38, 51,  7, 52, 53, 11,  0,  0,
        29, 12, 13, 20, 24, 16,  8,  0,  0, 32, 50, 34, 42, 45, 38, 46, 52,  6,
         1, 42, 44,  1, 56,  1, 34,  1, 35, 42, 38, 46,  1, 37, 38, 51,  1, 46,
        47, 53, 54, 38, 44, 44, 38, 51,  8,  1, 23, 47, 46,  1, 47, 46, 36, 44,
        38,  1, 54, 38, 53, 52,  1, 50, 66, 51, 47, 44, 72, 45, 38, 46, 52,  1,
        49, 53, 38,  1, 45, 34,  0, 36, 47, 53, 51, 42, 46, 38,  1, 66, 48, 47,
        53, 51, 38,  1, 32, 42, 44, 44, 38, 35, 50, 38, 49, 53, 42, 46,  6,  1,
        38, 52,  1, 44, 38, 51,  1, 34, 39, 39, 34, 42, 50, 38, 51,  1, 51, 47,
        46, 52,  1, 52, 38, 44, 44, 38, 45, 38, 46, 52,  1, 34, 54, 34, 46, 36,
        66, 38, 51,  6,  0, 49, 53, 38,  1, 43, 38,  1, 36, 50, 47, 42, 51,  1,
        49, 53,  3, 42, 44, 51,  1, 38, 53, 51, 51, 38, 46, 52,  1, 66, 52, 66,
         1, 45, 34, 50, 42, 66, 51,  1, 37, 65, 51,  1, 34, 53, 43, 47])

Dividimos los datos en conjuntos de entrenamiento y prueba:

n = int(0.9*len(data)) # 90% pour le train et 10% pour le test
train_data = data[:n]
test = data[n:]

Nota: En cada iteración, recorremos todo el dataset de forma secuencial.

Construcción del modelo#

¡Construyamos el modelo!

Según el artículo, la entrada (carácter) se codifica en one-hot y se suma al estado previo. Necesitamos dos capas fully connected:

  1. Primera capa: transforma \(x(t)\) en el estado oculto \(s(t)\).

  2. Segunda capa: convierte \(s(t)\) en la predicción \(y(t)\).

RNN

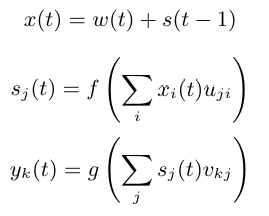
Ecuación del artículo: \(f\) = sigmoide, \(g\) = softmax.

Recomendación: El artículo original es claro y conciso. ¡Vale la pena leerlo!

class rnn(nn.Module): 
  def __init__(self,hidden_dim,vocab_size) -> None:
    super(rnn, self).__init__()
    self.hidden_to_hidden=nn.Linear(hidden_dim+vocab_size, hidden_dim)
    self.hidden_to_output=nn.Linear(hidden_dim, vocab_size)
    self.vocab_size=vocab_size
    self.hidden_dim=hidden_dim
    self.sigmoid=nn.Sigmoid() 
    
  # Le réseau prend en entrée le caractère actuel et le state précédent
  def forward(self, x,state):
    # On one-hot encode le caractère
    x = torch.nn.functional.one_hot(x, self.vocab_size).float()
    if state is None:
      # Si on a pas de state (début de la séquence), on initialise le state avec des petites valeurs aléatoires
      state = torch.randn(self.hidden_dim) * 0.1
    x = torch.cat((x, state), dim=-1)  # Concaténation de x et du state
    state = self.sigmoid(self.hidden_to_hidden(x)) # Calcul du nouveau state
    output = self.hidden_to_output(state) # Calcul de l'output
    # On renvoie l'output et le state pour le prochain pas de temps
    return output, state.detach() # detach() pour éviter de propager le gradient dans le state

Entrenamiento del modelo#

Parámetros de entrenamiento:

epochs = 10
lr=0.1
hidden_dim=128
model=rnn(hidden_dim,vocab_size)
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=lr)

¡Entrenemos el modelo!

for epoch in range(epochs):
    state=None
    running_loss = 0
    n=0
    for i in range(len(train_data)-1):
        x = train_data[i]
        y = train_data[i+1]
        optimizer.zero_grad()
        y_pred,state = model.forward(x,state)
        loss = criterion(y_pred, y)
        running_loss += loss.item()
        n+=1
        loss.backward()
        optimizer.step()

    print("Epoch: {0} \t Loss: {1:.8f}".format(epoch, running_loss/n))

Epoch: 0 	 Loss: 2.63949568
Epoch: 1 	 Loss: 2.16456994
Epoch: 2 	 Loss: 2.00850788
Epoch: 3 	 Loss: 1.91673251
Epoch: 4 	 Loss: 1.84440742
Epoch: 5 	 Loss: 1.78986003
Epoch: 6 	 Loss: 1.74923073
Epoch: 7 	 Loss: 1.71709289
Epoch: 8 	 Loss: 1.68791167
Epoch: 9 	 Loss: 1.66215199

Evaluamos el modelo con los datos de prueba:

state=None
running_loss = 0
n=0
for i in range(len(train_data)-1):
    with torch.no_grad():
        x = train_data[i]
        y = train_data[i+1]
        y_pred,state = model.forward(x,state)
        loss = criterion(y_pred, y)
        running_loss += loss.item()
        n+=1
print("Loss: {0:.8f}".format(running_loss/n))

Loss: 1.77312289

La pérdida (loss) en los datos de prueba es ligeramente mayor que en entrenamiento. El modelo presenta ligero overfitting.

Generación de texto#

Con el modelo entrenado, ¡podemos generar texto al estilo de Molière!

import torch.nn.functional as F 
moliere='.'
sequence_length=250
state=None
for i in range(sequence_length):
    x = torch.tensor(encode(moliere[-1]), dtype=torch.long).squeeze()
    y_pred,state = model.forward(x,state)
    probs=F.softmax(torch.squeeze(y_pred), dim=0)
    sample=torch.multinomial(probs, 1)
    moliere+=itos[sample.item()]
print(moliere)

.

VARDILE.

Vout on est nt, jes l'un ouint; sabhil.

LE DOCTE.

Si vous dicefalassîntes
GIRGIB.

MARGRIILÉ.

LE DOCTE. Jort; et
; bieu,
et je mu tu d'ais d'ai coupce!

SGÉLLÉ.

Il Sgnous elli massit que
Suis pluagil dés.
Cais téscompas: y totte demes

El resultado no es perfecto, pero se reconocen algunas palabras y una estructura de frases similar al archivo “moliere.txt”. ¡No está mal para una RNN de una sola capa!

¿Cómo mejorar los resultados? Algunas ideas:

  • Aumentar el número de capas o el tamaño de la capa oculta.

  • Usar embeddings en lugar de one-hot encoding.

  • Probar variantes de RNN como LSTM o GRU.

  • ~~Usar una arquitectura transformer~~ (¡spoiler!).

Limitaciones de las RNN#

Aunque las RNN fueron centrales en NLP y deep learning, tienen limitaciones que las hacen poco prácticas para modelos grandes:

  • Contexto teóricamente infinito, pero su estructura secuencial dificulta propagar información en secuencias largas.

  • Problema del vanishing gradient: los gradientes se desvanecen en secuencias largas.

  • Dificultad para paralelizar: los GPU están optimizados para cálculos paralelos, pero las RNN son inherentemente secuenciales (entrenamiento más lento).

  • Estructura fija: no siempre captura relaciones complejas entre datos.

Desde la llegada de los transformers, el uso de RNN ha disminuido significativamente.

Contents