Derivada y descenso del gradiente

Derivada y descenso del gradiente#

Este curso presenta el algoritmo de descenso del gradiente, un pilar fundamental del deep learning. Para comprenderlo bien, comencemos con un repaso sobre las derivadas.

import matplotlib.pyplot as plt 
import numpy as np

Comprensión intuitiva de la derivada#

Consideremos una función: \(f(x) = 2x^2 - 3x + 4\)

def f(x):
  return 2*x**2-3*x+4
f(3)

13

Grafiquemos esta función usando matplotlib.

xs = np.arange(-5, 5, 0.25)
ys = f(xs)
plt.plot(xs, ys)

[<matplotlib.lines.Line2D at 0x7ae9dcdf63d0>]
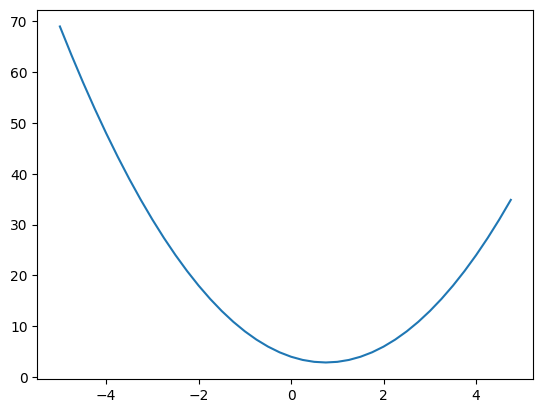
../_images/8ae53ec1c1a7a83c40158a7e0d6aeac20e0c0089b96c23bc11822f2fad3e62d5.png

La derivada proporciona la pendiente de la tangente a la curva en un punto dado. Para calcularla, utilizamos la siguiente fórmula: \(f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}\). Con un valor pequeño de \(h\), podemos estimar la pendiente de forma numérica.

Nota: La pendiente indica cómo varía \(y\) cuando \(x\) cambia. Por ejemplo, si \(x\) aumenta en 1 y \(y\) aumenta en 2, la pendiente es 2.

h=0.0001
x=-1.0
print("Dérivée en x=-1 : ", (f(x+h)-f(x))/h)
x=2.0
print("Dérivée en x=2 : ", (f(x+h)-f(x))/h)

Dérivée en x=-1 :  -6.999800000002665
Dérivée en x=2 :  5.000200000004895

El gráfico muestra que la pendiente es negativa en \(x = -1\) y positiva en \(x = 2\). El signo de la derivada indica la dirección de la pendiente, mientras que su valor absoluto refleja su intensidad. Verifiquemos esto con las derivadas comunes: Para \(f(x) = 2x^2 - 3x + 4\), obtenemos \(f'(x) = 4x - 3\). Así, \(f'(-1) \approx -7\) y \(f'(2) \approx 5\). Los resultados no son exactos porque \(h\) no es infinitamente pequeño.

# On définit deriv_f = f'(x)
def deriv_f(x):
  return 4*x-3

Fundamentos de la optimización mediante descenso del gradiente#

La optimización busca minimizar o maximizar una función objetivo. Para encontrar el mínimo, existen dos enfoques principales:

  1. Resolver \(f'(x) = 0\): \(4x - 3 = 0 \implies x = \frac{3}{4}\). En este caso, esto nos da el mínimo, pero no siempre es aplicable en general.

  2. Utilizar el descenso del gradiente: Partimos de un punto inicial, por ejemplo, \(x = 2\). Calculamos \(f'(2) = 5\). Una pendiente positiva indica que, si \(x\) aumenta, \(f(x)\) también lo hace (y viceversa). Para minimizar \(f(x)\), ajustamos \(x\) usando un factor \(\alpha\) (denominado tasa de aprendizaje). Obtenemos \(x_{nuevo} = x - \text{pendiente} \times \alpha = 2 - 5 \times 0.1 = 1.5\). Recalculamos \(f'(1.5) = 3\) (aún positiva), por lo que seguimos disminuyendo \(x\). El descenso del gradiente ajusta \(x\) iterativamente hasta alcanzar un mínimo, siempre considerando la pendiente en cada paso.

# Descente du gradient
x=2.0 # valeur aléatoire de x
alpha=0.01 # pas
iterations=250 # nombre d'itérations

for i in range(iterations):
  grad=deriv_f(x)
  if (grad>0):
    x=x-alpha
  elif(grad<0):
    x=x+alpha
  else:
    print("minimum found YAY, x = ",x)
print("approximate minimum found YAY, x = ",x)

approximate minimum found YAY, x =  0.7599999999999989

Obtenemos \(x \approx \frac{3}{4}\). Con un paso más pequeño (\(\alpha\)) y más iteraciones, podemos refinar el resultado.

La regla de la cadena#

Antes de avanzar, recordemos una regla matemática esencial para el deep learning: la regla de la cadena. Esta regla permite entrenar los parámetros de las capas ocultas de una red neuronal. Si \(y\) depende de \(u\), y \(u\) depende de \(x\), entonces: \(\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}\).

Tomemos un ejemplo con funciones dependientes: \(u = 2x^2 - x - 2\) \(y = 3u + 1\) Aplicando la regla de la cadena: \(\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}\), donde \(\frac{dy}{du} = 3\) y \(\frac{du}{dx} = 4x - 1\). Por lo tanto, \(\frac{dy}{dx} = 3(4x - 1) = 12x - 3\). Ahora sabemos cómo \(x\) afecta a \(y\), lo que nos permite aplicar el algoritmo de descenso del gradiente.

x=2.0
def deriv_y_x(x):
  return 6*x-3
for i in range(iterations):
  grad=deriv_y_x(x)
  if (grad>0):
    x=x-alpha
  elif(grad<0):
    x=x+alpha
  else:
    print("minimum found YAY, x = ",x)
print("approximate minimum found YAY, x = ",x)

approximate minimum found YAY, x =  0.49999999999999867

Optimización de múltiples variables#

Hasta ahora, hemos buscado el mínimo de una función con una sola variable \(x\). Una ventaja de los métodos de optimización es que podemos optimizar varias variables simultáneamente mediante el descenso del gradiente. Para ello, es necesario calcular la derivada con respecto a cada variable.

Consideremos un modelo con 3 variables: \(a\), \(b\) y \(c\): \(u = 3a^2 - 2a + b^2 + 1\) \(y = 2u + c\) Para aplicar el descenso del gradiente, calculamos \(\frac{dy}{da}\), \(\frac{dy}{db}\) y \(\frac{dy}{dc}\) usando la regla de la cadena:

  • Para \(a\): \(\frac{dy}{da} = \frac{dy}{du} \cdot \frac{du}{da} = 2(6a - 2) = 12a - 4\)

  • Para \(b\): \(\frac{dy}{db} = \frac{dy}{du} \cdot \frac{du}{db} = 2(2b) = 4b\)

  • Para \(c\): \(\frac{dy}{dc} = 1\)

Ahora ya podemos aplicar el algoritmo de descenso del gradiente.

def deriv_y_a(a):
  return 12*a-4
def deriv_y_b(b):
  return 4*b
def deriv_y_c(c):
  return 1

a=1.0
b=1.0
c=1.0
alpha=0.05
def deriv_y_x(x):
  return 6*x-3
for i in range(iterations):
  grad_a=deriv_y_a(a)
  grad_b=deriv_y_b(b)
  grad_c=deriv_y_c(b)
  if (grad_a>0):
    a=a-alpha
  else:
    a=a+alpha
  if (grad_b>0):
    b=b-alpha
  else:
    b=b+alpha
  if (grad_c>0):
    c=c-alpha
  else:
    c=c+alpha
print("approximate minimum found YAY, a = "+str(a)+" b = "+str(b)+" c = "+str(c))

approximate minimum found YAY, a = 0.29999999999999966 b = -3.191891195797325e-16 c = -11.50000000000003

Hemos encontrado valores que minimizan \(y\):

  • \(c\) tiende a menos infinito tras muchas iteraciones.

  • \(b\) converge a 0.

  • \(a\) alcanza un valor de 0.3.

Contents