Swin Transformer

Este notebook analiza el artículo Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. Propone una mejora de la arquitectura transformer con un diseño jerárquico adaptado a imágenes, similar a las redes neuronales convolucionales. La primera parte del notebook explica las propuestas del artículo una por una. La segunda parte presenta una implementación simplificada de la arquitectura.

Análisis del artículo.

La idea principal del artículo es aplicar el mecanismo de atención de manera jerárquica sobre partes cada vez más grandes de la imagen. Este enfoque se basa en varios fundamentos:

• El análisis de imágenes comienza con los detalles locales antes de considerar las relaciones entre todos los píxeles. Esto explica por qué las CNNs son tan eficientes.

• El hecho de que los tokens (patches) no se comuniquen con todos los demás mejora el tiempo de cómputo.

Arquitectura jerárquica

La arquitectura jerárquica del swin transformer se resume en la siguiente figura:

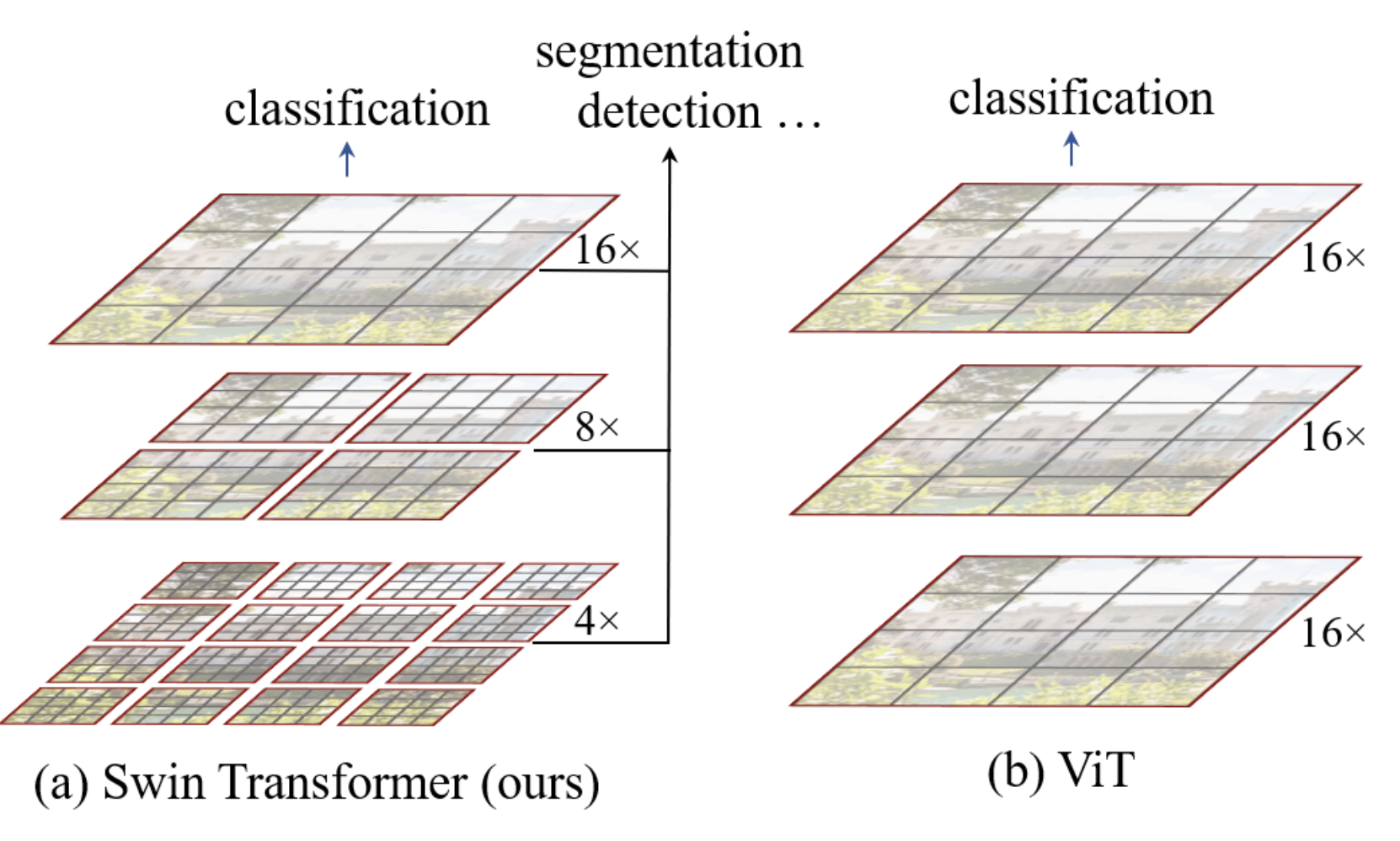
En nuestra implementación, el modelo ViT convierte los patches en tokens y aplica un transformer encoder a todos los elementos. Es una arquitectura simple y sin sesgo en los datos, aplicable a diversos tipos de datos.

La arquitectura swin añade un sesgo para mejorar su rendimiento con imágenes y acelerar el procesamiento. Como muestra la figura, la imagen se divide primero en pequeños patches (de tamaño \(4 \times 4\) en el artículo) agrupados en ventanas. La capa de atención se aplica solo a cada ventana de forma independiente. A medida que avanzamos en la red, la dimensión \(C\) (tamaño de los patches relativo a la imagen) y el tamaño de las ventanas aumentan hasta cubrir toda la imagen, con el mismo número de patches que la arquitectura ViT. Al igual que una CNN, la red procesa primero la información local y, progresivamente (con el aumento del campo receptivo), información cada vez más global. Esto se logra aumentando el número de filtros y reduciendo la resolución de la imagen.

Los nuevos bloques de transformer correspondientes se denominan Window Multi-Head Self-Attention (W-MSA en el artículo; nota: la M significa Multi-Head, no Masked).

Ventana corredera

En su analogía con las CNNs, los autores observaron que puede ser problemático dividir la imagen en ventanas con posiciones arbitrarias, ya que esto rompe la conexión entre píxeles vecinos ubicados en los bordes de las ventanas.

Para solucionar este problema, los autores proponen usar un sistema de ventanas desplazadas (shifting window) en cada bloque swin. Los bloques swin se organizan en pares, como se describe en la figura al inicio del notebook.

Así es como se ve una ventana desplazada:

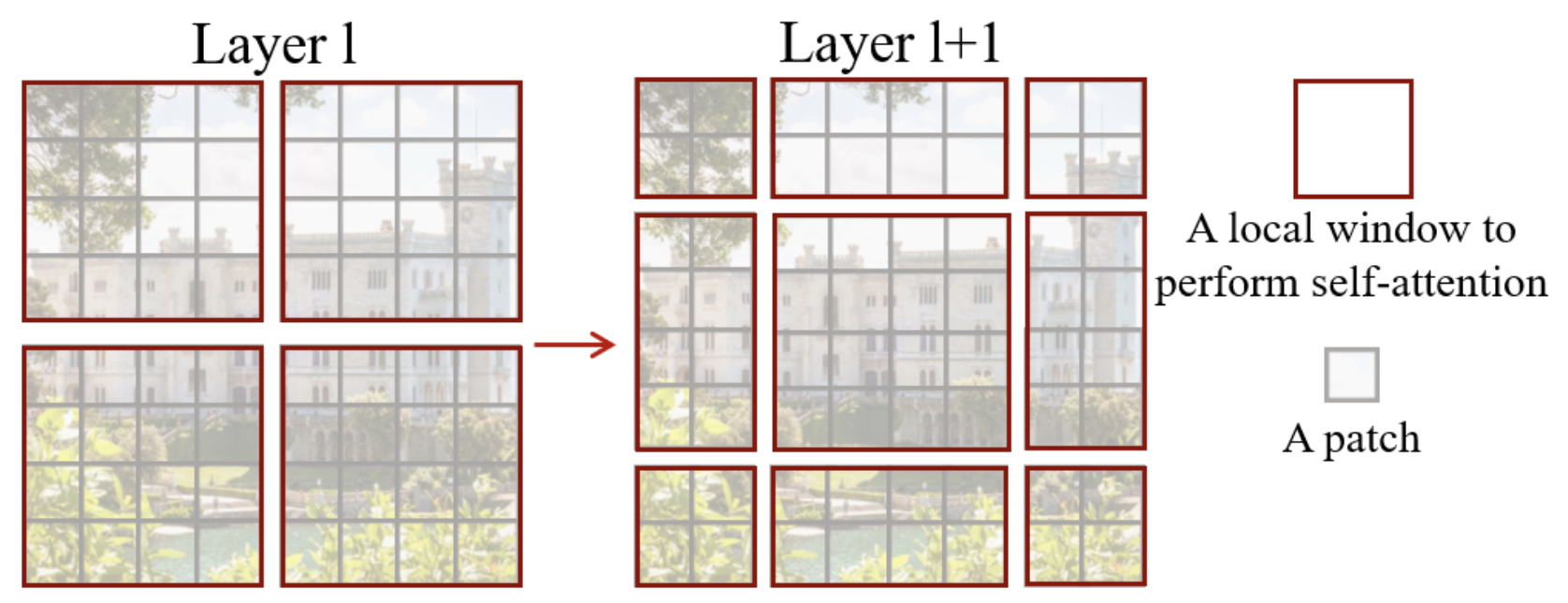
Como puede observarse, con esta técnica se pasa de ventanas de \(2 \times 2\) patches a \(3 \times 3\) (en general, de \(n \times n\) a \((n+1) \times (n+1)\)). Esto plantea problemas para el procesamiento en la red, especialmente en modo batch.

Los autores proponen incorporar un desplazamiento cíclico (cyclic shift), que consiste en aplicar esta operación a la imagen para permitir un procesamiento más eficiente:

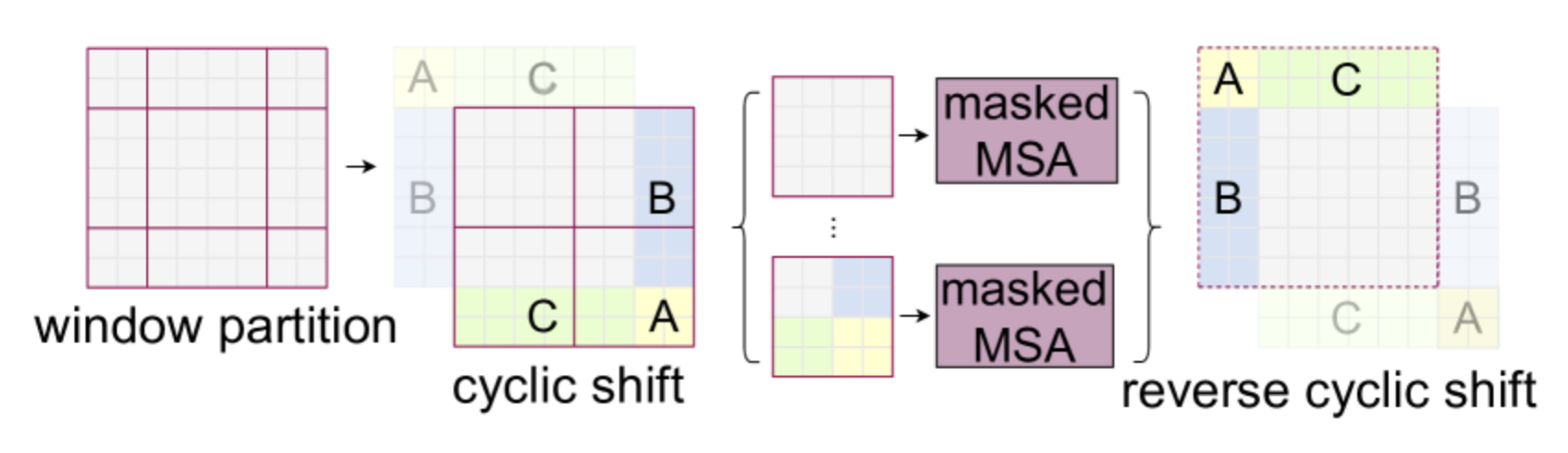
Tenga en cuenta que para usar este método es necesario enmascarar la información de los patches que no provienen de la misma parte de la imagen. Las partes blancas, amarillas, verdes y azules de la figura no se comunican entre sí gracias a una capa de atención enmascarada.

Sesgo de posición relativa

La arquitectura ViT utilizaba un position embedding absoluto para añadir información de posición a los diferentes patches. El problema de este método es que no captura las relaciones entre los patches, por lo que es menos eficiente con imágenes de diferentes resoluciones.

El swin transformer utiliza un sesgo de posición relativa para compensar esto. Este sesgo depende de la distancia relativa entre los diferentes patches y se añade cuando se calcula la atención entre dos patches. Su principal ventaja es mejorar la captura de relaciones espaciales y adaptarse a imágenes de diferentes resoluciones.

Detalles complementarios de la arquitectura

• Como se observa en la primera figura del notebook, hay más capas en la etapa 3 del swin transformer. Al aumentar el número de capas de la red, solo se incrementan las capas de la etapa 3, mientras que las demás permanecen fijas. Esto permite aprovechar la arquitectura swin (como el shifting) y, al mismo tiempo, mantener una profundidad suficiente para ser eficiente en términos de tiempo de procesamiento.

• Supongamos que cada ventana contiene patches de tamaño \(M \times M\). La complejidad computacional de una capa multi-head self-attention (MSA) y una capa window multi-head self-attention (W-MSA) para una imagen de \(h \times w\) patches es: \(\Omega(\text{MSA}) = 4hwC^2 + 2(h w)^2 C\) \(\Omega(\text{W-MSA}) = 4hwC^2 + 2M^2hwC\) La primera tiene una complejidad cuadrática, mientras que la segunda es lineal si \(M\) es fijo. La arquitectura swin permite ganar velocidad de procesamiento.

Implementación simplificada

Ahora pasaremos a la implementación en PyTorch del swin transformer. Algunas partes son bastante complejas de implementar y no las cubriremos aquí: la parte de ventanas desplazadas y el sesgo de posición relativa. Por lo tanto, nos limitaremos a implementar la arquitectura jerárquica.

Si desea consultar la implementación completa del swin transformer realizada por los autores, puede visitar su GitHub. Nuestra implementación se inspira en el código de los autores y retoma nuestra implementación del ViT.

import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision.transforms as T
import torchvision.datasets as datasets
import matplotlib.pyplot as plt

# Detection automatique du GPU
device = "cpu"
if torch.cuda.is_available():
    device = "cuda"
print(f"using device: {device}")

/home/aquilae/anaconda3/envs/dev/lib/python3.11/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
  from .autonotebook import tqdm as notebook_tqdm

using device: cuda

Conversión de imagen en parche

Pour la conversion de l’image en patch, nous reprenons notre fonction du notebook précédent :

def image_to_patches(image, patch_size):
    # On rajoute une dimension pour le batch
    B,C,_,_ = image.shape
    patches = image.unfold(2, patch_size, patch_size).unfold(3, patch_size, patch_size)
    patches = patches.permute(0,2, 3, 1, 4, 5).contiguous()
    patches = patches.view(B,-1, C, patch_size, patch_size)
    patches_flat = patches.flatten(2, 4)
    return patches_flat

Multi-head self-attention

En la implementación del swin, la capa multi-head self-attention no cambia con respecto a la implementación del ViT. Básicamente es la misma capa, pero lo que cambia es la forma en que se utiliza en el bloque swin.

Retomemos, entonces, nuestro código del notebook anterior:

class Head_enc(nn.Module):
    """ Couche de self-attention unique """
    def __init__(self, head_size,n_embd,dropout=0.2):
        super().__init__()
        self.key = nn.Linear(n_embd, head_size, bias=False)
        self.query = nn.Linear(n_embd, head_size, bias=False)
        self.value = nn.Linear(n_embd, head_size, bias=False)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        B,T,C = x.shape   
        k = self.key(x)   # (B,T,C)
        q = self.query(x) # (B,T,C)
        # Le * C**-0.5 correspond à la normalisation par la racine de head_size
        wei = q @ k.transpose(-2,-1) * C**-0.5 # (B, T, C) @ (B, C, T) -> (B, T, T)
        # On a supprimer le masquage du futur
        wei = F.softmax(wei, dim=-1) # (B, T, T)
        wei = self.dropout(wei)
        v = self.value(x) # (B,T,C)
        out = wei @ v # (B, T, T) @ (B, T, C) -> (B, T, C)
        return out

class MultiHeadAttention(nn.Module):
    """ Plusieurs couches de self attention en parallèle"""

    def __init__(self, num_heads, head_size,n_embd,dropout):
        super().__init__()
        # Création de num_head couches head_enc de taille head_size
        self.heads = nn.ModuleList([Head_enc(head_size,n_embd,dropout) for _ in range(num_heads)])
        self.proj = nn.Linear(n_embd, n_embd)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        out = torch.cat([h(x) for h in self.heads], dim=-1)
        out = self.dropout(self.proj(out))
        return out

Nota: Si se desea implementar el sesgo de posición relativa, habría que modificar la función, ya que este sesgo se añade directamente durante el cálculo de la atención (consulte el código fuente para más detalles).

Feed forward layer

Lo mismo ocurre con la capa feed forward, que permanece igual:

class FeedFoward(nn.Module):

    def __init__(self, n_embd,dropout):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(n_embd, 4 * n_embd),
            nn.GELU(),
            nn.Linear(4 * n_embd, n_embd),
            nn.Dropout(dropout),
        )

    def forward(self, x):
        return self.net(x)

Implementación del bloque swin

Comencemos implementando la función para dividir nuestra imagen en ventanas. Para ello, convertiremos nuestra \(x\) a una dimensión \(B \times H \times W \times C\) en lugar de \(B \times T \times C\). Luego, transformaremos nuestro tensor en múltiples ventanas que se procesarán en la dimensión batch (para tratar cada ventana de forma independiente).

def window_partition(x, window_size,input_resolution):
    B,_,C = x.shape
    H,W = input_resolution
    x = x.view(B, H, W, C)
    B, H, W, C = x.shape
    x = x.view(B, H // window_size, window_size, W // window_size, window_size, C)
    windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size, window_size, C)
    return windows

Por ejemplo, supongamos que, como en la implementación del artículo, dividimos nuestra imagen de tamaño 224 en patches de \(4 \times 4\). Esto nos dará \(224/4 \times 224/4\) patches, es decir, 3136, que luego se proyectarán en una dimensión de embedding \(C\) de tamaño 96 (para swin-T y swin-S). Vamos a separarlos en \(M=7\) ventanas, lo que nos dará el siguiente tensor:

# Pour un batch de taille 2
window_size = 7
n_embed = 96
dummy=torch.randn(2,3136,n_embed)
windows=window_partition(dummy,window_size,(56,56))
print(windows.shape)

torch.Size([128, 7, 7, 96])

Antes de pasarlo a la capa de atención, debemos convertirlo nuevamente a una dimensión \(B \times T \times C\).

windows=windows.view(-1, window_size * window_size, n_embed)
print(windows.shape)

torch.Size([128, 49, 96])

Luego podremos aplicar nuestra capa de atención para realizar el self-attention en todas las ventanas de forma independiente. Una vez hecho esto, hay que aplicar la transformación inversa para volver a un formato sin ventanas:

def window_reverse(windows, window_size,input_resolution):
    H,W=input_resolution
    B = int(windows.shape[0] / (H * W / window_size / window_size))
    x = windows.view(B, H // window_size, W // window_size, window_size, window_size, -1)
    x = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(B, H, W, -1)
    return x

windows=window_reverse(windows,window_size,(56,56))
print(windows.shape)
# et revenir en format BxTxC
windows=windows.view(2,3136,n_embed)
print(windows.shape)

torch.Size([2, 56, 56, 96])
torch.Size([2, 3136, 96])

Acabamos de implementar los elementos fundamentales para el procesamiento por ventanas (jerarquía del swin transformer). Ahora podemos construir nuestro bloque swin que agrupa todas estas transformaciones:

class swinblock(nn.Module):
  def __init__(self, n_embd,n_head,input_resolution,window_size,dropout=0.) -> None:
    super().__init__()
    head_size = n_embd // n_head
    self.sa = MultiHeadAttention(n_head, head_size,n_embd,dropout)
    self.ffwd = FeedFoward(n_embd,dropout)
    self.ln1 = nn.LayerNorm(n_embd)
    self.ln2 = nn.LayerNorm(n_embd)
    self.input_resolution = input_resolution
    self.window_size = window_size
    self.n_embd = n_embd
    
  def forward(self,x):
    B,T,C = x.shape
    x=window_partition(x, self.window_size,self.input_resolution)
    x=self.ln1(x)
    x=x.view(-1, self.window_size * self.window_size, self.n_embd)
    x=self.sa(x)
    x=window_reverse(x,self.window_size,self.input_resolution)
    x=x.view(B,T,self.n_embd)
    x=x+self.ffwd(self.ln2(x))
    return x

Fusión de parches

En la arquitectura jerárquica del swin transformer, cada vez que aumentamos nuestro campo receptivo (reduciendo el número de ventanas), concatenamos los 4 patches adyacentes de tamaño \(C\) en una dimensión \(4C\) y luego aplicamos una capa lineal para reducirla a una dimensión más pequeña de \(2C\). Esto reduce el número de tokens en un factor de 4 cada vez que disminuimos el número de ventanas. Podemos recuperar los patches adyacentes de la siguiente manera:

# Reprenons un exemple de nos 56x56 patchs
dummy=torch.randn(2,3136,n_embed)
B,T,C = dummy.shape
H,W=T**0.5,T**0.5
dummy=dummy.view(2,56,56,n_embed)
# En python, 0::2 prend un élément sur 2 à partir de 0, 1::2 prend un élément sur 2 à partir de 1
# De cette manière, on peut récupérer les à intervalles réguliers 
dummy0 = dummy[:, 0::2, 0::2, :]  # B H/2 W/2 C
dummy1 = dummy[:, 1::2, 0::2, :]  # B H/2 W/2 C
dummy2 = dummy[:, 0::2, 1::2, :]  # B H/2 W/2 C
dummy3 = dummy[:, 1::2, 1::2, :]  # B H/2 W/2 C
print(dummy0.shape)

torch.Size([2, 28, 28, 96])

Luego concatenaremos nuestros patches adyacentes:

dummy = torch.cat([dummy0, dummy1, dummy2, dummy3], -1)  # B H/2 W/2 4*C
print(dummy.shape)
# On repasse en BxTxC
dummy = dummy.view(B, -1, 4 * C)
print(dummy.shape)

torch.Size([2, 28, 28, 384])
torch.Size([2, 784, 384])

Hemos dividido por cuatro el número de patches mientras aumentamos los canales en un factor de 4. Ahora aplicamos la capa lineal para reducir el número de canales.

layer = nn.Linear(4 * C, 2 * C, bias=False)
dummy = layer(dummy)
print(dummy.shape)

torch.Size([2, 784, 192])

Y así, tenemos todos los elementos para construir nuestra capa de merging:

class PatchMerging(nn.Module):

    def __init__(self, input_resolution, in_channels, norm_layer=nn.LayerNorm):
        super().__init__()
        self.input_resolution = input_resolution
        self.in_channels = in_channels
        self.reduction = nn.Linear(4 * in_channels, 2 * in_channels, bias=False)
        self.norm = norm_layer(4 * in_channels)

    def forward(self, x):

        H, W = self.input_resolution
        B, L, C = x.shape
        assert L == H * W, "input feature has wrong size"
        assert H % 2 == 0 and W % 2 == 0, f"x size ({H}*{W}) are not even."

        x = x.view(B, H, W, C)
        x0 = x[:, 0::2, 0::2, :]  # B H/2 W/2 C
        x1 = x[:, 1::2, 0::2, :]  # B H/2 W/2 C
        x2 = x[:, 0::2, 1::2, :]  # B H/2 W/2 C
        x3 = x[:, 1::2, 1::2, :]  # B H/2 W/2 C
        x = torch.cat([x0, x1, x2, x3], -1)  # B H/2 W/2 4*C
        x = x.view(B, -1, 4 * C)  # B H/2*W/2 4*C
        x = self.norm(x)
        x = self.reduction(x)
        return x

Y ya tenemos todos los elementos para construir nuestra capa de merging:

Para el swin transformer, es complicado añadir un cls_token en la implementación. Por eso usaremos el otro método mencionado en el notebook anterior: el adaptive average pooling. Esto nos permite tener una salida de tamaño fijo, independientemente del tamaño de la imagen de entrada.

# 3 blocs de 2 couches au lieu de 4 car CIFAR-10 a de plus petites images
class SwinTransformer(nn.Module):
  def __init__(self,n_embed,patch_size,C,window_size,num_heads,img_dim=[16,8,4],depths=[2,2,2]) -> None:
    super().__init__()
    self.patch_size = patch_size
    self.proj_layer = nn.Linear(C*patch_size*patch_size, n_embed)
    input_resolution = [(img_dim[0],img_dim[0]),(img_dim[1],img_dim[1]),(img_dim[2],img_dim[2])]
    self.blocks1 = nn.Sequential(*[swinblock(n_embed,num_heads,input_resolution[0],window_size) for _ in range(depths[0])])
    self.down1 = PatchMerging(input_resolution[0],in_channels=n_embed)
    self.blocks2 = nn.Sequential(*[swinblock(n_embed*2,num_heads,input_resolution[1],window_size) for _ in range(depths[1])])
    self.down2 = PatchMerging(input_resolution[1],in_channels=n_embed*2)
    self.blocks3 = nn.Sequential(*[swinblock(n_embed*4,num_heads,input_resolution[2],window_size) for _ in range(depths[2])])
    self.classi_head = nn.Linear(n_embed*4, 10)
    self.avgpool = nn.AdaptiveAvgPool1d(1)
  
  def forward(self,x):
    x = image_to_patches(x,self.patch_size)
    x = self.proj_layer(x)
    x = self.blocks1(x)
    x = self.down1(x)
    x = self.blocks2(x)
    x = self.down2(x)
    x = self.blocks3(x)
    x = self.avgpool(x.transpose(1, 2)).flatten(1)
    x = self.classi_head(x)
    return x

Formación sobre Imagenette

Para probar nuestro modelo, utilizaremos nuevamente CIFAR-10, aunque el pequeño tamaño de las imágenes no se adapte necesariamente bien a la arquitectura jerárquica.

Nota: Puede seleccionar una subparte del conjunto de datos para acelerar el entrenamiento.

import torchvision.transforms as T
import torchvision.datasets as datasets
from torch.utils.data import DataLoader

classes = ('plane', 'car', 'bird', 'cat','deer', 'dog', 'frog', 'horse', 'ship', 'truck')
# Transformation des données, normalisation et transformation en tensor pytorch
transform = T.Compose([T.ToTensor(),T.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
dataset = datasets.CIFAR10(root='./../data', train=True,download=False, transform=transform)
# indices = torch.randperm(len(dataset))[:5000]
# dataset = torch.utils.data.Subset(dataset, indices)

testdataset = datasets.CIFAR10(root='./../data', train=False,download=False, transform=transform)
# indices = torch.randperm(len(testdataset))[:1000]
# testdataset = torch.utils.data.Subset(testdataset, indices)
print("taille d'une image : ",dataset[0][0].shape)


#Création des dataloaders pour le train, validation et test
train_dataset, val_dataset=torch.utils.data.random_split(dataset, [0.8,0.2])
print("taille du train dataset : ",len(train_dataset))
print("taille du val dataset : ",len(val_dataset))
print("taille du test dataset : ",len(testdataset))
train_loader = DataLoader(train_dataset, batch_size=16,shuffle=True, num_workers=2)
val_loader= DataLoader(val_dataset, batch_size=16,shuffle=True, num_workers=2)
test_loader = DataLoader(testdataset, batch_size=16,shuffle=False, num_workers=2)

taille d'une image :  torch.Size([3, 32, 32])
taille du train dataset :  40000
taille du val dataset :  10000
taille du test dataset :  10000

patch_size = 2
n_embed = 24
n_head = 4
C=3 
window_size = 4

epochs = 10
lr = 0.0001 #1e-3

model = SwinTransformer(n_embed,patch_size,C,window_size,n_head,img_dim=[16,8,4],depths=[2,2,2]).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=lr)

for epoch in range(epochs):
    model.train()
    loss_train = 0
    for i, (images, labels) in enumerate(train_loader):
        images, labels = images.to(device), labels.to(device)
        optimizer.zero_grad()
        output = model(images)
        loss = F.cross_entropy(output, labels)
        loss_train += loss.item()
        loss.backward()
        optimizer.step()
        
    model.eval()
    correct = 0
    total = 0
    loss_val = 0
    with torch.no_grad():
        for images, labels in val_loader:
            images, labels = images.to(device), labels.to(device)
            outputs = model(images)
            loss_val += F.cross_entropy(outputs, labels).item()
            _, predicted = torch.max(outputs.data, 1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()

    print(f"Epoch {epoch}, loss train {loss_train/len(train_loader)}, loss val {loss_val/len(val_loader)},précision {100 * correct / total}")

Epoch 0, loss train 1.9195597559928894, loss val 1.803518475151062,précision 33.94
Epoch 1, loss train 1.7417401003360748, loss val 1.6992134885787964,précision 37.84
Epoch 2, loss train 1.651085284280777, loss val 1.6203388486862182,précision 40.53
Epoch 3, loss train 1.5808091670751572, loss val 1.5558069843292237,précision 43.03
Epoch 4, loss train 1.522760990524292, loss val 1.5169190183639527,précision 44.3
Epoch 5, loss train 1.4789127678394318, loss val 1.4665142657279968,précision 47.02
Epoch 6, loss train 1.4392719486951828, loss val 1.4568698994636535,précision 47.65
Epoch 7, loss train 1.4014943064451217, loss val 1.4456377569198609,précision 48.14
Epoch 8, loss train 1.3745941290140151, loss val 1.4345624563694,précision 48.38
Epoch 9, loss train 1.3492228104948998, loss val 1.398228020954132,précision 50.04

El entrenamiento ha finalizado; obtenemos una precisión del 50% en los datos de validación.

Veamos ahora los resultados en nuestros datos de prueba:

model.eval()
correct = 0
total = 0
with torch.no_grad():
    for images, labels in test_loader:
        images, labels = images.to(device), labels.to(device)
        outputs = model(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print(f"Précision {100 * correct / total}")

Précision 49.6

¡La precisión es aproximadamente similar a la de los datos de validación!

Nota: Los resultados no son muy buenos por varias razones. En primer lugar, estamos procesando imágenes pequeñas, mientras que la arquitectura jerárquica del swin transformer está diseñada para manejar imágenes de mayores dimensiones. Además, nuestra implementación es bastante minimalista, ya que faltan dos elementos clave de la arquitectura swin: la parte de ventanas desplazadas y el sesgo de posición relativa. El objetivo de este notebook era dar una intuición sobre el funcionamiento de la arquitectura swin y no proponer una implementación perfecta ;)