Autoencoder para desruido

Intuición

¿Qué es el desruido?

El desruido consiste en eliminar el ruido no deseado de una imagen. Es una tarea crucial en el procesamiento de imágenes. Nuestro objetivo es introducir en la red una imagen con ruido y obtener a la salida una imagen limpia.

Figura extraída del artículo.

Uso de un autoencoder para el desruido

Para utilizar la arquitectura del autoencoder en esta tarea, basta con introducir en el decodificador una imagen con ruido (que hemos generado), hacer que reconstruya la imagen y comparar la imagen reconstruida con la imagen original sin ruido.

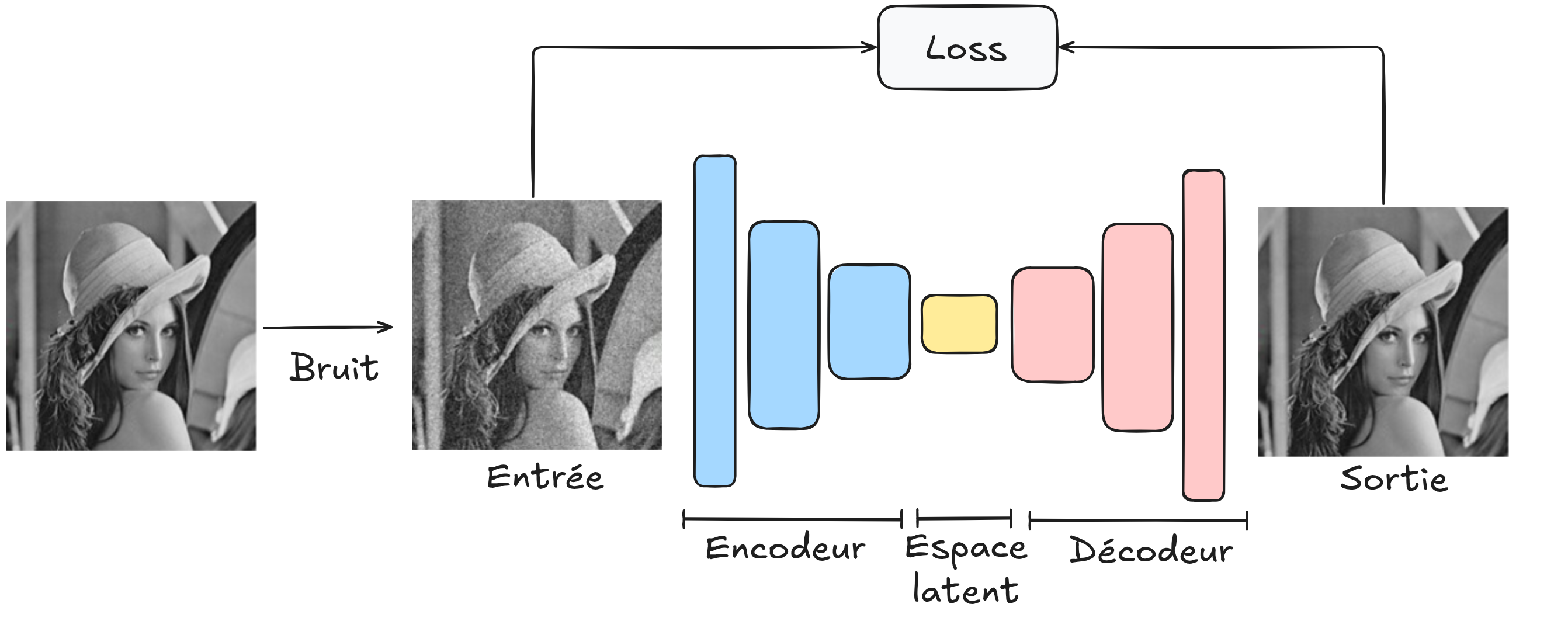
Con esta arquitectura, buscamos crear un modelo de desruido robusto capaz de eliminar el ruido de cualquier imagen. Para su entrenamiento, se necesitará una gran base de datos de imágenes y asegurarse de que el ruido generado sea similar al que se encuentra en imágenes reales.

Desruido con un autoencoder en PyTorch

Una vez más, utilizamos el conjunto de datos MNIST. Vamos a generar ruido artificial en las imágenes y entrenar a nuestro autoencoder para eliminar este ruido y obtener una imagen limpia.

import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision.transforms as T
from torchvision import datasets
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt

Conjunto de datos y cargador de datos

transform=T.ToTensor() # Pour convertir les éléments en tensor torch directement
dataset = datasets.MNIST(root='./../data', train=True, download=True,transform=transform)
test_dataset = datasets.MNIST(root='./../data', train=False,transform=transform)
train_dataset, validation_dataset=torch.utils.data.random_split(dataset, [0.8,0.2])
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
val_loader= DataLoader(validation_dataset, batch_size=64, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False)

Generación de ruido

Hagamos un ejemplo de aplicación de ruido para visualizar la degradación de la imagen según el nivel de ruido.

image,_=dataset[0]
# Le paramètre dans le np.sqrt correspond à la variance désirée donc np.sqrt(...) est l'écart type
# torch.randn génére des valeurs aléatoire extraites d'une distribution gaussienne de mean 0 et variance 1
imageNoisy1 = image + np.sqrt(0.001)*torch.randn(1, 28, 28)
imageNoisy2 = image + np.sqrt(0.01)*torch.randn(1, 28, 28)
imageNoisy3 = image + np.sqrt(0.1)*torch.randn(1, 28, 28)

plt.subplot(2, 2, 1)
plt.imshow(image.squeeze().numpy(), cmap='gray')
plt.title("Image originale")

plt.subplot(2, 2, 2)
plt.imshow(imageNoisy1.squeeze().numpy(), cmap='gray')
plt.title("Faible bruit")

plt.subplot(2, 2, 3)
plt.imshow(imageNoisy2.squeeze().numpy(), cmap='gray')
plt.title("Bruit moyen")

plt.subplot(2, 2, 4)
plt.imshow(imageNoisy3.squeeze().numpy(), cmap='gray')
plt.title("Fort bruit")

plt.tight_layout()
plt.show()

Vamos a utilizar un nivel de ruido medio durante el entrenamiento. Luego, podremos observar cómo se comporta nuestro autoencoder de desruido con otros niveles de ruido.

Creación de nuestro modelo

Para esta tarea compleja, utilizamos un autoencoder convolucional.

# Nous réutilisons les fonctions introduites dans l'exemple de segmentation du cours 3 
def conv_relu_bn(input_channels, output_channels, kernel_size, stride, padding):
  return nn.Sequential(
    nn.Conv2d(input_channels, output_channels, kernel_size, stride, padding),
    nn.ReLU(),
    nn.BatchNorm2d(output_channels,momentum=0.01)
  )
    
def convT_relu_bn(input_channels, output_channels, kernel_size, stride, padding):
  return nn.Sequential(
    nn.ConvTranspose2d(input_channels, output_channels, kernel_size, stride, padding),
    nn.ReLU(),
    nn.BatchNorm2d(output_channels,momentum=0.01)
  )
    
    
class ae_conv(nn.Module):
  def __init__(self, *args, **kwargs) -> None:
    super().__init__(*args, **kwargs)

    self.encoder = nn.Sequential( # Sequential permet de groupe une série de transformation
      conv_relu_bn(1,8,kernel_size=3,stride=2,padding=1),
      conv_relu_bn(8,16,kernel_size=3,stride=2,padding=1),
      conv_relu_bn(16,32,kernel_size=3,stride=1,padding=1),
    )
    self.decoder = nn.Sequential(
      convT_relu_bn(32,16,kernel_size=4,stride=2,padding=1),
      convT_relu_bn(16,8,kernel_size=4,stride=2,padding=1),
      nn.Conv2d(8,1,kernel_size=3,stride=1,padding=1),
      nn.Sigmoid()
    )
  
  def forward(self,x): 
    x = self.encoder(x)
    denoise = self.decoder(x)
    return denoise

model = ae_conv() # Couches d'entrée de taille 2, deux couches cachées de 16 neurones et un neurone de sortie
print("Nombre de paramètres", sum(p.numel() for p in model.parameters()))

Nombre de paramètres 16385

Entrenamiento del modelo

criterion = nn.MSELoss()
epochs=10
learning_rate=0.001
optimizer=torch.optim.Adam(model.parameters(),lr=learning_rate)

for i in range(epochs):
  loss_train=0
  for images, _ in train_loader:
    images=images+np.sqrt(0.01)*torch.randn(images.shape)
    recons=model(images)
    loss=criterion(recons,images)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    loss_train+=loss   
  if i % 1 == 0:
    print(f"step {i} train loss {loss_train/len(train_loader)}")
  loss_val=0    
  for images, _ in val_loader:
    with torch.no_grad():
      images=images+np.sqrt(0.01)*torch.randn(images.shape)
      recons=model(images)
      loss=criterion(recons,images)
      loss_val+=loss 
  if i % 1 == 0:
    print(f"step {i} val loss {loss_val/len(val_loader)}")

step 0 train loss 0.0253756046295166
step 0 val loss 0.010878251865506172
step 1 train loss 0.00976449716836214
step 1 val loss 0.008979358710348606
step 2 train loss 0.00827114749699831
step 2 val loss 0.007526080124080181
step 3 train loss 0.00706455297768116
step 3 val loss 0.0066648973152041435
step 4 train loss 0.006312613375484943
step 4 val loss 0.005955129396170378
step 5 train loss 0.00576859712600708
step 5 val loss 0.005603262223303318
step 6 train loss 0.0055686105042696
step 6 val loss 0.005487256217747927
step 7 train loss 0.0054872902110219
step 7 val loss 0.005444051697850227
step 8 train loss 0.0054359594359993935
step 8 val loss 0.005416598636657
step 9 train loss 0.005397486500442028
step 9 val loss 0.005359680857509375

images,_=next(iter(test_loader))
variance=0.01
#Isolons un élément
fig, axs = plt.subplots(2, 3, figsize=(10, 6)) 
for i in range(2):
  image=images[i].unsqueeze(0)
  noisy_image=image+np.sqrt(variance)*torch.randn(image.shape)

  with torch.no_grad():
      recons=model(noisy_image)

  # Image d'origine
  axs[i][0].imshow(noisy_image[0].squeeze().cpu().numpy(), cmap='gray')
  axs[i][0].set_title('Image d\'origine')
  axs[i][0].axis('off')

  # Image reconstruite
  axs[i][1].imshow(recons[0].squeeze().cpu().numpy(), cmap='gray')
  axs[i][1].set_title('Image reconstruite')
  axs[i][1].axis('off')

  axs[i][2].imshow(image[0].squeeze().cpu().numpy(), cmap='gray')
  axs[i][2].set_title('Image de base')
  axs[i][2].axis('off')
plt.show()

Los resultados de nuestro desruido son bastante buenos, aunque quedan algunos artefactos. Al variar el parámetro de varianza, puedes visualizar qué es capaz de hacer el autoencoder de desruido con otros niveles de ruido.

Ejercicio

Puedes intentar entrenar el modelo con imágenes que tengan un nivel de ruido aleatorio (dentro de ciertos valores de varianza) para ver si el modelo es capaz de generalizar a cualquier tipo de ruido gaussiano en ese intervalo. Es posible que necesites hacer el modelo más complejo y añadir más epochs durante el entrenamiento.

U-Net: También puedes probar la arquitectura U-Net (ver clase 3 sobre segmentación) para la tarea de desruido y comparar los resultados con el autoencoder.